Continuous shrinkage prior revisited: a collapsing behavior and remedy

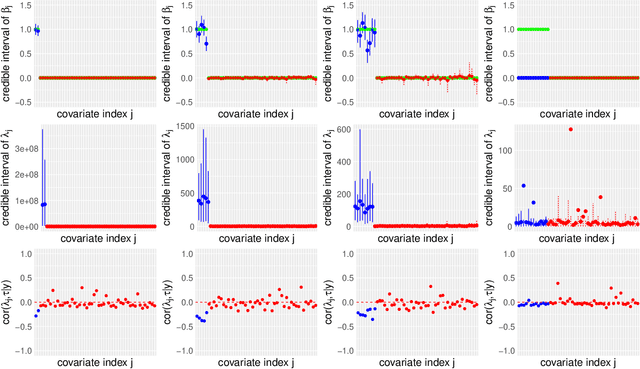
Modern genomic studies are increasingly focused on identifying more and more genes clinically associated with a health response. Commonly used Bayesian shrinkage priors are designed primarily to detect only a handful of signals when the dimension of the predictors is very high. In this article, we investigate the performance of a popular continuous shrinkage prior in the presence of relatively large number of true signals. We draw attention to an undesirable phenomenon; the posterior mean is rendered very close to a null vector, caused by a sharp underestimation of the global-scale parameter. The phenomenon is triggered by the absence of a tail-index controlling mechanism in the Bayesian shrinkage priors. We provide a remedy by developing a global-local-tail shrinkage prior which can automatically learn the tail-index and can provide accurate inference even in the presence of moderately large number of signals. The collapsing behavior of the Horseshoe with its remedy is exemplified in numerical examples and in two gene expression datasets.