Stacey: Promoting Stochastic Steepest Descent via Accelerated $\ell_p$-Smooth Nonconvex Optimization

While popular optimization methods such as SGD, AdamW, and Lion depend on steepest descent updates in either $\ell_2$ or $\ell_\infty$ norms, there remains a critical gap in handling the non-Euclidean structure observed in modern deep networks training. In this work, we address this need by introducing a new accelerated $\ell_p$ steepest descent algorithm, called Stacey, which uses interpolated primal-dual iterate sequences to effectively navigate non-Euclidean smooth optimization tasks. In addition to providing novel theoretical guarantees for the foundations of our algorithm, we empirically compare our approach against these popular methods on tasks including image classification and language model (LLM) pretraining, demonstrating both faster convergence and higher final accuracy. We further evaluate different values of $p$ across various models and datasets, underscoring the importance and efficiency of non-Euclidean approaches over standard Euclidean methods. Code can be found at https://github.com/xinyuluo8561/Stacey .

Inference Acceleration of Autoregressive Normalizing Flows by Selective Jacobi Decoding

Normalizing flows are promising generative models with advantages such as theoretical rigor, analytical log-likelihood computation, and end-to-end training. However, the architectural constraints to ensure invertibility and tractable Jacobian computation limit their expressive power and practical usability. Recent advancements utilize autoregressive modeling, significantly enhancing expressive power and generation quality. However, such sequential modeling inherently restricts parallel computation during inference, leading to slow generation that impedes practical deployment. In this paper, we first identify that strict sequential dependency in inference is unnecessary to generate high-quality samples. We observe that patches in sequential modeling can also be approximated without strictly conditioning on all preceding patches. Moreover, the models tend to exhibit low dependency redundancy in the initial layer and higher redundancy in subsequent layers. Leveraging these observations, we propose a selective Jacobi decoding (SeJD) strategy that accelerates autoregressive inference through parallel iterative optimization. Theoretical analyses demonstrate the method's superlinear convergence rate and guarantee that the number of iterations required is no greater than the original sequential approach. Empirical evaluations across multiple datasets validate the generality and effectiveness of our acceleration technique. Experiments demonstrate substantial speed improvements up to 4.7 times faster inference while keeping the generation quality and fidelity.

Sherlock: Self-Correcting Reasoning in Vision-Language Models

Reasoning Vision-Language Models (VLMs) have shown promising performance on complex multimodal tasks. However, they still face significant challenges: they are highly sensitive to reasoning errors, require large volumes of annotated data or accurate verifiers, and struggle to generalize beyond specific domains. To address these limitations, we explore self-correction as a strategy to enhance reasoning VLMs. We first conduct an in-depth analysis of reasoning VLMs' self-correction abilities and identify key gaps. Based on our findings, we introduce Sherlock, a self-correction and self-improvement training framework. Sherlock introduces a trajectory-level self-correction objective, a preference data construction method based on visual perturbation, and a dynamic $\beta$ for preference tuning. Once the model acquires self-correction capabilities using only 20k randomly sampled annotated data, it continues to self-improve without external supervision. Built on the Llama3.2-Vision-11B model, Sherlock achieves remarkable results across eight benchmarks, reaching an average accuracy of 64.1 with direct generation and 65.4 after self-correction. It outperforms LLaVA-CoT (63.2), Mulberry (63.9), and LlamaV-o1 (63.4) while using less than 20% of the annotated data.

Entropy-Guided Sampling of Flat Modes in Discrete Spaces

Sampling from flat modes in discrete spaces is a crucial yet underexplored problem. Flat modes represent robust solutions and have broad applications in combinatorial optimization and discrete generative modeling. However, existing sampling algorithms often overlook the mode volume and struggle to capture flat modes effectively. To address this limitation, we propose \emph{Entropic Discrete Langevin Proposal} (EDLP), which incorporates local entropy into the sampling process through a continuous auxiliary variable under a joint distribution. The local entropy term guides the discrete sampler toward flat modes with a small overhead. We provide non-asymptotic convergence guarantees for EDLP in locally log-concave discrete distributions. Empirically, our method consistently outperforms traditional approaches across tasks that require sampling from flat basins, including Bernoulli distribution, restricted Boltzmann machines, combinatorial optimization, and binary neural networks.

Energy-Based Reward Models for Robust Language Model Alignment

Reward models (RMs) are essential for aligning Large Language Models (LLMs) with human preferences. However, they often struggle with capturing complex human preferences and generalizing to unseen data. To address these challenges, we introduce Energy-Based Reward Model (EBRM), a lightweight post-hoc refinement framework that enhances RM robustness and generalization. EBRM models the reward distribution explicitly, capturing uncertainty in human preferences and mitigating the impact of noisy or misaligned annotations. It achieves this through conflict-aware data filtering, label-noise-aware contrastive training, and hybrid initialization. Notably, EBRM enhances RMs without retraining, making it computationally efficient and adaptable across different models and tasks. Empirical evaluations on RM benchmarks demonstrate significant improvements in both robustness and generalization, achieving up to a 5.97% improvement in safety-critical alignment tasks compared to standard RMs. Furthermore, reinforcement learning experiments confirm that our refined rewards enhance alignment quality, effectively delaying reward hacking. These results demonstrate our approach as a scalable and effective enhancement for existing RMs and alignment pipelines. The code is available at EBRM.

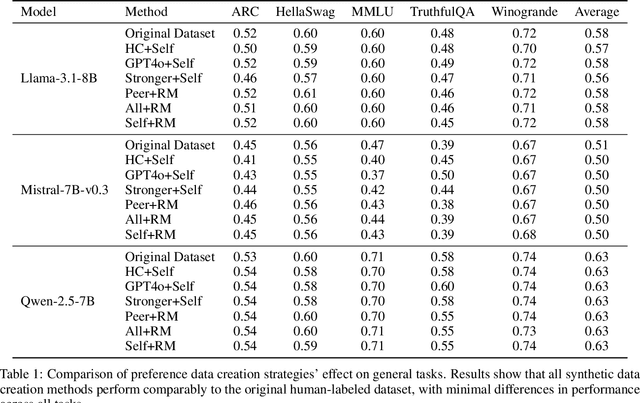
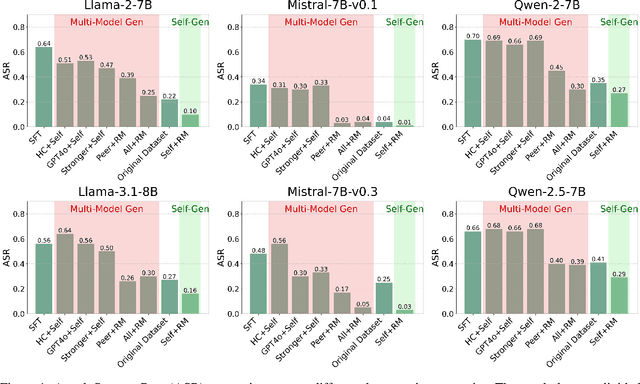
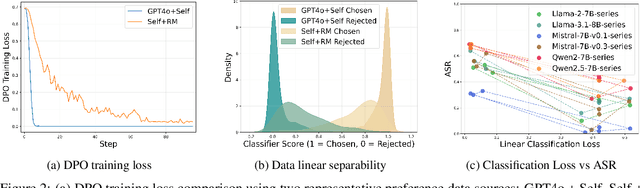
More is Less: The Pitfalls of Multi-Model Synthetic Preference Data in DPO Safety Alignment

Aligning large language models (LLMs) with human values is an increasingly critical step in post-training. Direct Preference Optimization (DPO) has emerged as a simple, yet effective alternative to reinforcement learning from human feedback (RLHF). Synthetic preference data with its low cost and high quality enable effective alignment through single- or multi-model generated preference data. Our study reveals a striking, safety-specific phenomenon associated with DPO alignment: Although multi-model generated data enhances performance on general tasks (ARC, Hellaswag, MMLU, TruthfulQA, Winogrande) by providing diverse responses, it also tends to facilitate reward hacking during training. This can lead to a high attack success rate (ASR) when models encounter jailbreaking prompts. The issue is particularly pronounced when employing stronger models like GPT-4o or larger models in the same family to generate chosen responses paired with target model self-generated rejected responses, resulting in dramatically poorer safety outcomes. Furthermore, with respect to safety, using solely self-generated responses (single-model generation) for both chosen and rejected pairs significantly outperforms configurations that incorporate responses from stronger models, whether used directly as chosen data or as part of a multi-model response pool. We demonstrate that multi-model preference data exhibits high linear separability between chosen and rejected responses, which allows models to exploit superficial cues rather than internalizing robust safety constraints. Our experiments, conducted on models from the Llama, Mistral, and Qwen families, consistently validate these findings.

Reheated Gradient-based Discrete Sampling for Combinatorial Optimization

Recently, gradient-based discrete sampling has emerged as a highly efficient, general-purpose solver for various combinatorial optimization (CO) problems, achieving performance comparable to or surpassing the popular data-driven approaches. However, we identify a critical issue in these methods, which we term ''wandering in contours''. This behavior refers to sampling new different solutions that share very similar objective values for a long time, leading to computational inefficiency and suboptimal exploration of potential solutions. In this paper, we introduce a novel reheating mechanism inspired by the concept of critical temperature and specific heat in physics, aimed at overcoming this limitation. Empirically, our method demonstrates superiority over existing sampling-based and data-driven algorithms across a diverse array of CO problems.

Bayesian Computation in Deep Learning

This review paper is intended for the 2nd edition of the Handbook of Markov chain Monte Carlo. We provide an introduction to approximate inference techniques as Bayesian computation methods applied to deep learning models. We organize the chapter by presenting popular computational methods for Bayesian neural networks and deep generative models, explaining their unique challenges in posterior inference as well as the solutions.

Optimal Stochastic Trace Estimation in Generative Modeling

Hutchinson estimators are widely employed in training divergence-based likelihoods for diffusion models to ensure optimal transport (OT) properties. However, this estimator often suffers from high variance and scalability concerns. To address these challenges, we investigate Hutch++, an optimal stochastic trace estimator for generative models, designed to minimize training variance while maintaining transport optimality. Hutch++ is particularly effective for handling ill-conditioned matrices with large condition numbers, which commonly arise when high-dimensional data exhibits a low-dimensional structure. To mitigate the need for frequent and costly QR decompositions, we propose practical schemes that balance frequency and accuracy, backed by theoretical guarantees. Our analysis demonstrates that Hutch++ leads to generations of higher quality. Furthermore, this method exhibits effective variance reduction in various applications, including simulations, conditional time series forecasts, and image generation.

CoT-UQ: Improving Response-wise Uncertainty Quantification in LLMs with Chain-of-Thought

Large language models (LLMs) excel in many tasks but struggle to accurately quantify uncertainty in their generated responses. This limitation makes it challenging to detect misinformation and ensure reliable decision-making. Existing uncertainty quantification (UQ) methods for LLMs are primarily prompt-wise rather than response-wise, often requiring multiple response samples, which incurs high computational costs. Moreover, LLMs have been shown to be overconfident, particularly when using reasoning steps to derive their answers. In this work, we propose CoT-UQ, a response-wise UQ framework that integrates LLMs' inherent reasoning capabilities through Chain-of-Thought (CoT) into the UQ process. CoT-UQ captures critical information during inference by extracting keywords from each reasoning step and assessing their importance to the final answer. This key reasoning information is then aggregated to produce a final uncertainty estimate. We conduct extensive experiments based on LLaMA Family with model sizes varying from 8B to 13B across logical and mathematical reasoning tasks. Experimental results demonstrate that CoT-UQ significantly outperforms existing UQ methods, achieving an average improvement of 5.9% AUROC compared to current UQ methods. The code is available at: https://github.com/ZBox1005/CoT-UQ.