Ananth Grama
More is Less: The Pitfalls of Multi-Model Synthetic Preference Data in DPO Safety Alignment
Apr 03, 2025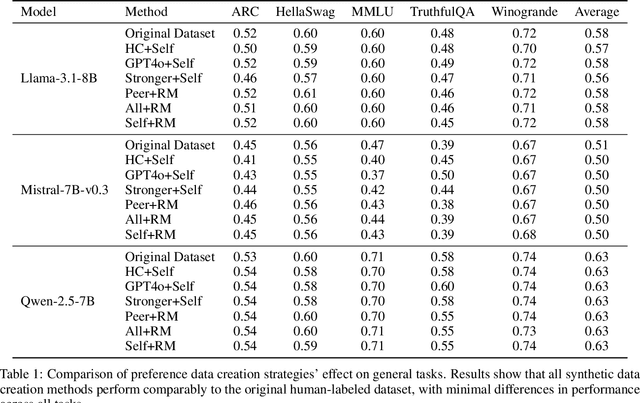
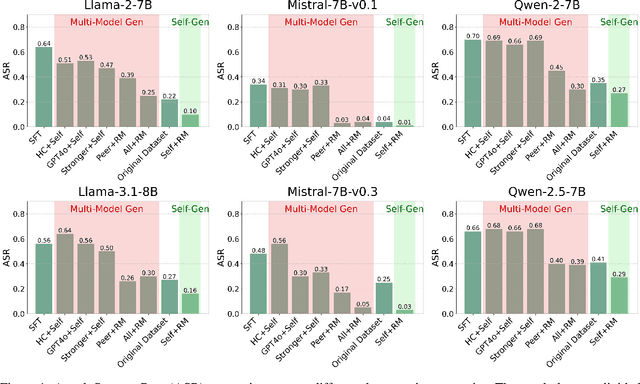
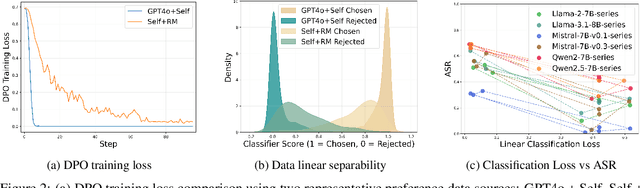

Abstract:Aligning large language models (LLMs) with human values is an increasingly critical step in post-training. Direct Preference Optimization (DPO) has emerged as a simple, yet effective alternative to reinforcement learning from human feedback (RLHF). Synthetic preference data with its low cost and high quality enable effective alignment through single- or multi-model generated preference data. Our study reveals a striking, safety-specific phenomenon associated with DPO alignment: Although multi-model generated data enhances performance on general tasks (ARC, Hellaswag, MMLU, TruthfulQA, Winogrande) by providing diverse responses, it also tends to facilitate reward hacking during training. This can lead to a high attack success rate (ASR) when models encounter jailbreaking prompts. The issue is particularly pronounced when employing stronger models like GPT-4o or larger models in the same family to generate chosen responses paired with target model self-generated rejected responses, resulting in dramatically poorer safety outcomes. Furthermore, with respect to safety, using solely self-generated responses (single-model generation) for both chosen and rejected pairs significantly outperforms configurations that incorporate responses from stronger models, whether used directly as chosen data or as part of a multi-model response pool. We demonstrate that multi-model preference data exhibits high linear separability between chosen and rejected responses, which allows models to exploit superficial cues rather than internalizing robust safety constraints. Our experiments, conducted on models from the Llama, Mistral, and Qwen families, consistently validate these findings.
No Free Lunch: Fundamental Limits of Learning Non-Hallucinating Generative Models
Oct 24, 2024Abstract:Generative models have shown impressive capabilities in synthesizing high-quality outputs across various domains. However, a persistent challenge is the occurrence of "hallucinations", where the model produces outputs that are plausible but invalid. While empirical strategies have been explored to mitigate this issue, a rigorous theoretical understanding remains elusive. In this paper, we develop a theoretical framework to analyze the learnability of non-hallucinating generative models from a learning-theoretic perspective. Our results reveal that non-hallucinating learning is statistically impossible when relying solely on the training dataset, even for a hypothesis class of size two and when the entire training set is truthful. To overcome these limitations, we show that incorporating inductive biases aligned with the actual facts into the learning process is essential. We provide a systematic approach to achieve this by restricting the facts set to a concept class of finite VC-dimension and demonstrate its effectiveness under various learning paradigms. Although our findings are primarily conceptual, they represent a first step towards a principled approach to addressing hallucinations in learning generative models.
Generalized Learning of Coefficients in Spectral Graph Convolutional Networks
Sep 07, 2024Abstract:Spectral Graph Convolutional Networks (GCNs) have gained popularity in graph machine learning applications due, in part, to their flexibility in specification of network propagation rules. These propagation rules are often constructed as polynomial filters whose coefficients are learned using label information during training. In contrast to learned polynomial filters, explicit filter functions are useful in capturing relationships between network topology and distribution of labels across the network. A number of algorithms incorporating either approach have been proposed; however the relationship between filter functions and polynomial approximations is not fully resolved. This is largely due to the ill-conditioned nature of the linear systems that must be solved to derive polynomial approximations of filter functions. To address this challenge, we propose a novel Arnoldi orthonormalization-based algorithm, along with a unifying approach, called G-Arnoldi-GCN that can efficiently and effectively approximate a given filter function with a polynomial. We evaluate G-Arnoldi-GCN in the context of multi-class node classification across ten datasets with diverse topological characteristics. Our experiments show that G-Arnoldi-GCN consistently outperforms state-of-the-art methods when suitable filter functions are employed. Overall, G-Arnoldi-GCN opens important new directions in graph machine learning by enabling the explicit design and application of diverse filter functions. Code link: https://anonymous.4open.science/r/GArnoldi-GCN-F7E2/README.md
Deconvolving Complex Neuronal Networks into Interpretable Task-Specific Connectomes
Jun 28, 2024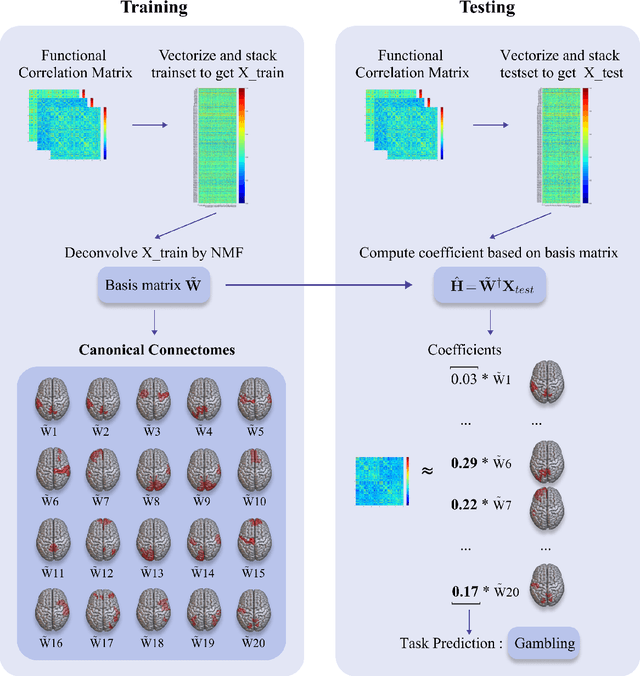
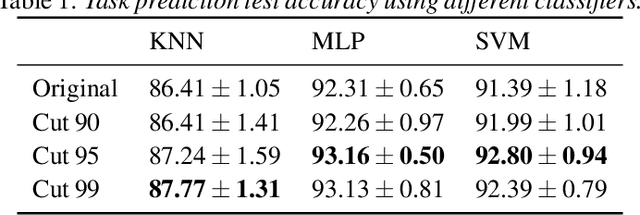
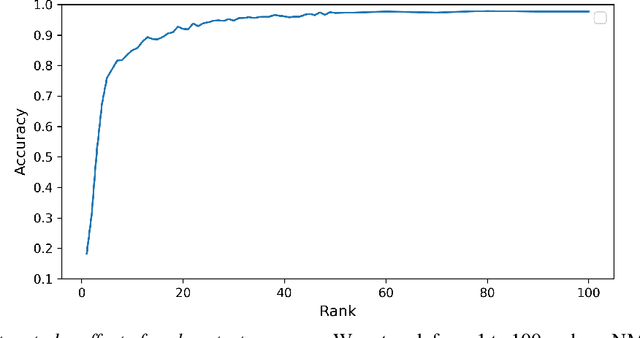

Abstract:Task-specific functional MRI (fMRI) images provide excellent modalities for studying the neuronal basis of cognitive processes. We use fMRI data to formulate and solve the problem of deconvolving task-specific aggregate neuronal networks into a set of basic building blocks called canonical networks, to use these networks for functional characterization, and to characterize the physiological basis of these responses by mapping them to regions of the brain. Our results show excellent task-specificity of canonical networks, i.e., the expression of a small number of canonical networks can be used to accurately predict tasks; generalizability across cohorts, i.e., canonical networks are conserved across diverse populations, studies, and acquisition protocols; and that canonical networks have strong anatomical and physiological basis. From a methods perspective, the problem of identifying these canonical networks poses challenges rooted in the high dimensionality, small sample size, acquisition variability, and noise. Our deconvolution technique is based on non-negative matrix factorization (NMF) that identifies canonical networks as factors of a suitably constructed matrix. We demonstrate that our method scales to large datasets, yields stable and accurate factors, and is robust to noise.
Cascade Reward Sampling for Efficient Decoding-Time Alignment
Jun 24, 2024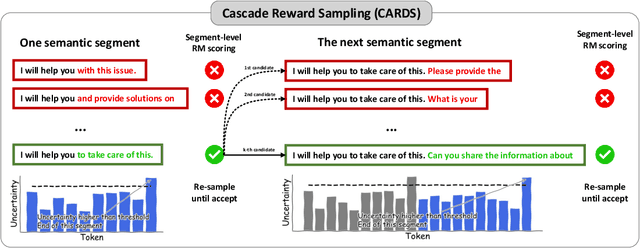

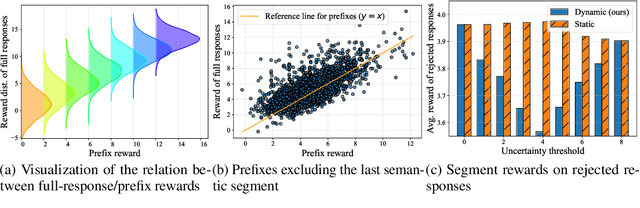
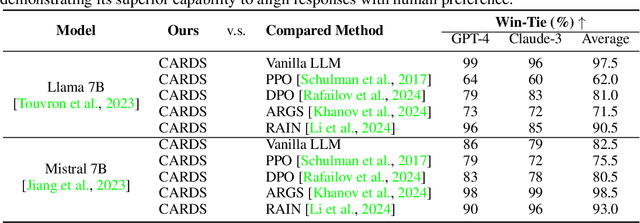
Abstract:Aligning large language models (LLMs) with human preferences is critical for their deployment. Recently, decoding-time alignment has emerged as an effective plug-and-play technique that requires no fine-tuning of model parameters. However, generating text that achieves both high reward and high likelihood remains a significant challenge. Existing methods often fail to generate high-reward text or incur substantial computational costs. In this paper, we propose Cascade Reward Sampling (CARDS) to address both issues, guaranteeing the generation of high-reward and high-likelihood text with significantly low costs. Based on our analysis of reward models (RMs) on incomplete text and our observation that high-reward prefixes induce high-reward complete text, we use rejection sampling to iteratively generate small semantic segments to form such prefixes. The segment length is dynamically determined by the predictive uncertainty of LLMs. This strategy guarantees desirable prefixes for subsequent generations and significantly reduces wasteful token re-generations and the number of reward model scoring. Our experiments demonstrate substantial gains in both generation efficiency and alignment ratings compared to the baselines, achieving five times faster text generation and 99\% win-ties in GPT-4/Claude-3 helpfulness evaluation.
Robust Online Classification: From Estimation to Denoising
Sep 04, 2023Abstract:We study online classification in the presence of noisy labels. The noise mechanism is modeled by a general kernel that specifies, for any feature-label pair, a (known) set of distributions over noisy labels. At each time step, an adversary selects an unknown distribution from the distribution set specified by the kernel based on the actual feature-label pair, and generates the noisy label from the selected distribution. The learner then makes a prediction based on the actual features and noisy labels observed thus far, and incurs loss $1$ if the prediction differs from the underlying truth (and $0$ otherwise). The prediction quality is quantified through minimax risk, which computes the cumulative loss over a finite horizon $T$. We show that for a wide range of natural noise kernels, adversarially selected features, and finite class of labeling functions, minimax risk can be upper bounded independent of the time horizon and logarithmic in the size of labeling function class. We then extend these results to inifinite classes and stochastically generated features via the concept of stochastic sequential covering. Our results extend and encompass findings of Ben-David et al. (2009) through substantial generality, and provide intuitive understanding through a novel reduction to online conditional distribution estimation.
Online Learning in Dynamically Changing Environments
Jan 31, 2023
Abstract:We study the problem of online learning and online regret minimization when samples are drawn from a general unknown non-stationary process. We introduce the concept of a dynamic changing process with cost $K$, where the conditional marginals of the process can vary arbitrarily, but that the number of different conditional marginals is bounded by $K$ over $T$ rounds. For such processes we prove a tight (upto $\sqrt{\log T}$ factor) bound $O(\sqrt{KT\cdot\mathsf{VC}(\mathcal{H})\log T})$ for the expected worst case regret of any finite VC-dimensional class $\mathcal{H}$ under absolute loss (i.e., the expected miss-classification loss). We then improve this bound for general mixable losses, by establishing a tight (up to $\log^3 T$ factor) regret bound $O(K\cdot\mathsf{VC}(\mathcal{H})\log^3 T)$. We extend these results to general smooth adversary processes with unknown reference measure by showing a sub-linear regret bound for $1$-dimensional threshold functions under a general bounded convex loss. Our results can be viewed as a first step towards regret analysis with non-stationary samples in the distribution blind (universal) regime. This also brings a new viewpoint that shifts the study of complexity of the hypothesis classes to the study of the complexity of processes generating data.
Expected Worst Case Regret via Stochastic Sequential Covering
Sep 17, 2022
Abstract:We study the problem of sequential prediction and online minimax regret with stochastically generated features under a general loss function. We introduce a notion of expected worst case minimax regret that generalizes and encompasses prior known minimax regrets. For such minimax regrets we establish tight upper bounds via a novel concept of stochastic global sequential covering. We show that for a hypothesis class of VC-dimension $\mathsf{VC}$ and $i.i.d.$ generated features of length $T$, the cardinality of the stochastic global sequential covering can be upper bounded with high probability (whp) by $e^{O(\mathsf{VC} \cdot \log^2 T)}$. We then improve this bound by introducing a new complexity measure called the Star-Littlestone dimension, and show that classes with Star-Littlestone dimension $\mathsf{SL}$ admit a stochastic global sequential covering of order $e^{O(\mathsf{SL} \cdot \log T)}$. We further establish upper bounds for real valued classes with finite fat-shattering numbers. Finally, by applying information-theoretic tools of the fixed design minimax regrets, we provide lower bounds for the expected worst case minimax regret. We demonstrate the effectiveness of our approach by establishing tight bounds on the expected worst case minimax regrets for logarithmic loss and general mixable losses.
Precise Regret Bounds for Log-loss via a Truncated Bayesian Algorithm
May 07, 2022
Abstract:We study the sequential general online regression, known also as the sequential probability assignments, under logarithmic loss when compared against a broad class of experts. We focus on obtaining tight, often matching, lower and upper bounds for the sequential minimax regret that are defined as the excess loss it incurs over a class of experts. After proving a general upper bound, we consider some specific classes of experts from Lipschitz class to bounded Hessian class and derive matching lower and upper bounds with provably optimal constants. Our bounds work for a wide range of values of the data dimension and the number of rounds. To derive lower bounds, we use tools from information theory (e.g., Shtarkov sum) and for upper bounds, we resort to new "smooth truncated covering" of the class of experts. This allows us to find constructive proofs by applying a simple and novel truncated Bayesian algorithm. Our proofs are substantially simpler than the existing ones and yet provide tighter (and often optimal) bounds.
CKH: Causal Knowledge Hierarchy for Estimating Structural Causal Models from Data and Priors
Apr 28, 2022
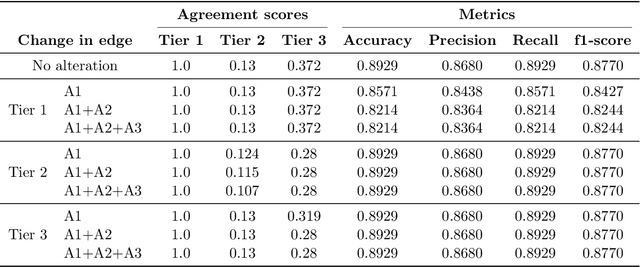
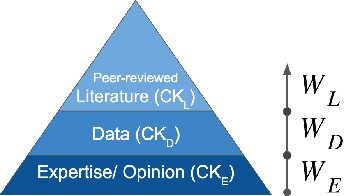

Abstract:Structural causal models (SCMs) provide a principled approach to identifying causation from observational and experimental data in disciplines ranging from economics to medicine. SCMs, however, require domain knowledge, which is typically represented as graphical models. A key challenge in this context is the absence of a methodological framework for encoding priors (background knowledge) into causal models in a systematic manner. We propose an abstraction called causal knowledge hierarchy (CKH) for encoding priors into causal models. Our approach is based on the foundation of "levels of evidence" in medicine, with a focus on confidence in causal information. Using CKH, we present a methodological framework for encoding causal priors from various data sources and combining them to derive an SCM. We evaluate our approach on a simulated dataset and demonstrate overall performance compared to the ground truth causal model with sensitivity analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge