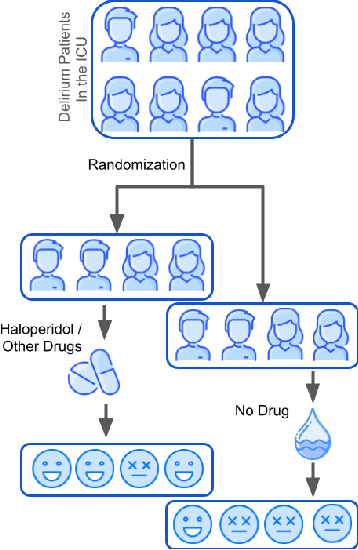
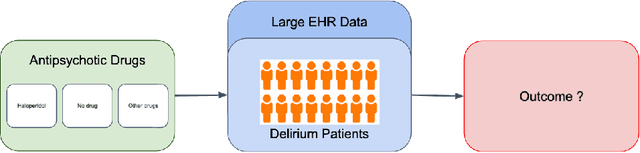
Causal Discovery on the Effect of Antipsychotic Drugs on Delirium Patients in the ICU using Large EHR Dataset

Delirium occurs in about 80% cases in the Intensive Care Unit (ICU) and is associated with a longer hospital stay, increased mortality and other related issues. Delirium does not have any biomarker-based diagnosis and is commonly treated with antipsychotic drugs (APD). However, multiple studies have shown controversy over the efficacy or safety of APD in treating delirium. Since randomized controlled trials (RCT) are costly and time-expensive, we aim to approach the research question of the efficacy of APD in the treatment of delirium using retrospective cohort analysis. We plan to use the Causal inference framework to look for the underlying causal structure model, leveraging the availability of large observational data on ICU patients. To explore safety outcomes associated with APD, we aim to build a causal model for delirium in the ICU using large observational data sets connecting various covariates correlated with delirium. We utilized the MIMIC III database, an extensive electronic health records (EHR) dataset with 53,423 distinct hospital admissions. Our null hypothesis is: there is no significant difference in outcomes for delirium patients under different drug-group in the ICU. Through our exploratory, machine learning based and causal analysis, we had findings such as: mean length-of-stay and max length-of-stay is higher for patients in Haloperidol drug group, and haloperidol group has a higher rate of death in a year compared to other two-groups. Our generated causal model explicitly shows the functional relationships between different covariates. For future work, we plan to do time-varying analysis on the dataset.

Pragmatic Clinical Trials in the Rubric of Structural Causal Models

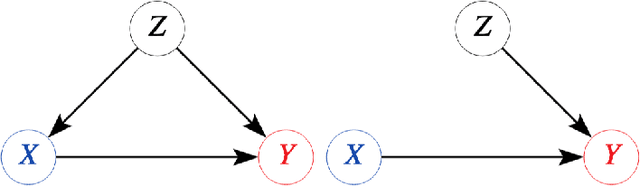
Explanatory studies, such as randomized controlled trials, are targeted to extract the true causal effect of interventions on outcomes and are by design adjusted for covariates through randomization. On the contrary, observational studies are a representation of events that occurred without intervention. Both can be illustrated using the Structural Causal Model (SCM), and do-calculus can be employed to estimate the causal effects. Pragmatic clinical trials (PCT) fall between these two ends of the trial design spectra and are thus hard to define. Due to its pragmatic nature, no standardized representation of PCT through SCM has been yet established. In this paper, we approach this problem by proposing a generalized representation of PCT under the rubric of structural causal models (SCM). We discuss different analysis techniques commonly employed in PCT using the proposed graphical model, such as intention-to-treat, as-treated, and per-protocol analysis. To show the application of our proposed approach, we leverage an experimental dataset from a pragmatic clinical trial. Our proposition of SCM through PCT creates a pathway to leveraging do-calculus and related mathematical operations on clinical datasets.

CKH: Causal Knowledge Hierarchy for Estimating Structural Causal Models from Data and Priors

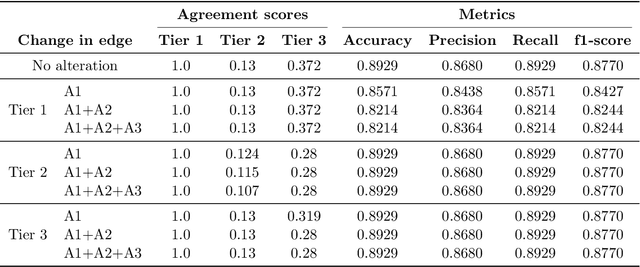
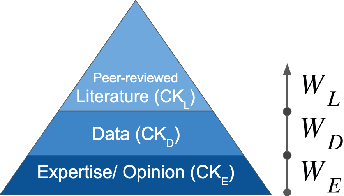
Structural causal models (SCMs) provide a principled approach to identifying causation from observational and experimental data in disciplines ranging from economics to medicine. SCMs, however, require domain knowledge, which is typically represented as graphical models. A key challenge in this context is the absence of a methodological framework for encoding priors (background knowledge) into causal models in a systematic manner. We propose an abstraction called causal knowledge hierarchy (CKH) for encoding priors into causal models. Our approach is based on the foundation of "levels of evidence" in medicine, with a focus on confidence in causal information. Using CKH, we present a methodological framework for encoding causal priors from various data sources and combining them to derive an SCM. We evaluate our approach on a simulated dataset and demonstrate overall performance compared to the ground truth causal model with sensitivity analysis.

A Causally Formulated Hazard Ratio Estimation through Backdoor Adjustment on Structural Causal Model

Identifying causal relationships for a treatment intervention is a fundamental problem in health sciences. Randomized controlled trials (RCTs) are considered the gold standard for identifying causal relationships. However, recent advancements in the theory of causal inference based on the foundations of structural causal models (SCMs) have allowed the identification of causal relationships from observational data, under certain assumptions. Survival analysis provides standard measures, such as the hazard ratio, to quantify the effects of an intervention. While hazard ratios are widely used in clinical and epidemiological studies for RCTs, a principled approach does not exist to compute hazard ratios for observational studies with SCMs. In this work, we review existing approaches to compute hazard ratios as well as their causal interpretation, if it exists. We also propose a novel approach to compute hazard ratios from observational studies using backdoor adjustment through SCMs and do-calculus. Finally, we evaluate the approach using experimental data for Ewing's sarcoma.