CKH: Causal Knowledge Hierarchy for Estimating Structural Causal Models from Data and Priors

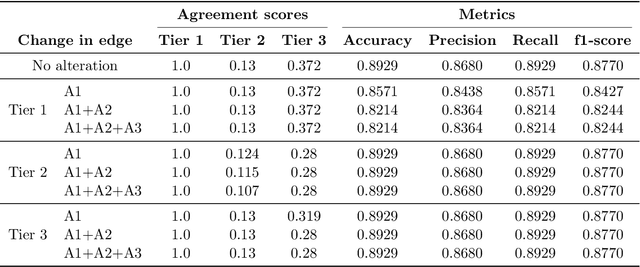
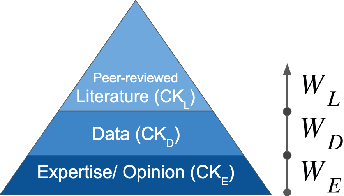
Structural causal models (SCMs) provide a principled approach to identifying causation from observational and experimental data in disciplines ranging from economics to medicine. SCMs, however, require domain knowledge, which is typically represented as graphical models. A key challenge in this context is the absence of a methodological framework for encoding priors (background knowledge) into causal models in a systematic manner. We propose an abstraction called causal knowledge hierarchy (CKH) for encoding priors into causal models. Our approach is based on the foundation of "levels of evidence" in medicine, with a focus on confidence in causal information. Using CKH, we present a methodological framework for encoding causal priors from various data sources and combining them to derive an SCM. We evaluate our approach on a simulated dataset and demonstrate overall performance compared to the ground truth causal model with sensitivity analysis.

Distributed Second-order Convex Optimization

Convex optimization problems arise frequently in diverse machine learning (ML) applications. First-order methods, i.e., those that solely rely on the gradient information, are most commonly used to solve these problems. This choice is motivated by their simplicity and low per-iteration cost. Second-order methods that rely on curvature information through the dense Hessian matrix have, thus far, proven to be prohibitively expensive at scale, both in terms of computational and memory requirements. We present a novel multi-GPU distributed formulation of a second order (Newton-type) solver for convex finite sum minimization problems for multi-class classification. Our distributed formulation relies on the Alternating Direction of Multipliers Method (ADMM), which requires only one round of communication per-iteration -- significantly reducing communication overheads, while incurring minimal convergence overhead. By leveraging the computational capabilities of GPUs, we demonstrate that per-iteration costs of Newton-type methods can be significantly reduced to be on-par with, if not better than, state-of-the-art first-order alternatives. Given their significantly faster convergence rates, we demonstrate that our methods can process large data-sets in much shorter time (orders of magnitude in many cases) compared to existing first and second order methods, while yielding similar test-accuracy results.