Memory Efficient And Minimax Distribution Estimation Under Wasserstein Distance Using Bayesian Histograms

We study Bayesian histograms for distribution estimation on $[0,1]^d$ under the Wasserstein $W_v, 1 \leq v < \infty$ distance in the i.i.d sampling regime. We newly show that when $d < 2v$, histograms possess a special \textit{memory efficiency} property, whereby in reference to the sample size $n$, order $n^{d/2v}$ bins are needed to obtain minimax rate optimality. This result holds for the posterior mean histogram and with respect to posterior contraction: under the class of Borel probability measures and some classes of smooth densities. The attained memory footprint overcomes existing minimax optimal procedures by a polynomial factor in $n$; for example an $n^{1 - d/2v}$ factor reduction in the footprint when compared to the empirical measure, a minimax estimator in the Borel probability measure class. Additionally constructing both the posterior mean histogram and the posterior itself can be done super--linearly in $n$. Due to the popularity of the $W_1,W_2$ metrics and the coverage provided by the $d < 2v$ case, our results are of most practical interest in the $(d=1,v =1,2), (d=2,v=2), (d=3,v=2)$ settings and we provide simulations demonstrating the theory in several of these instances.

Spatio-temporal extreme event modeling of terror insurgencies

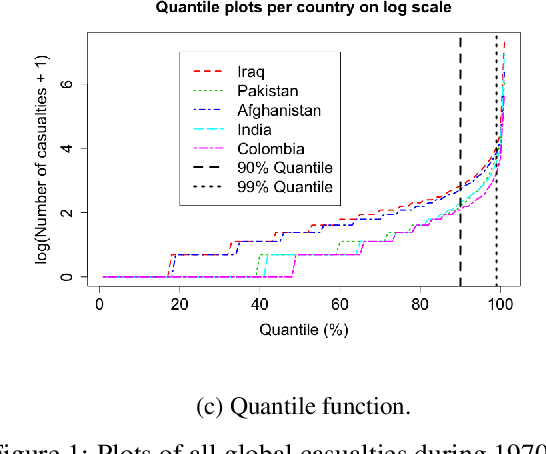
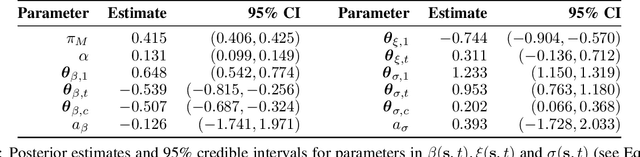
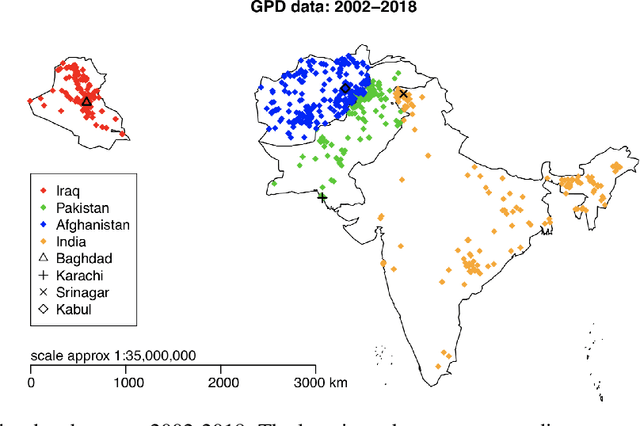
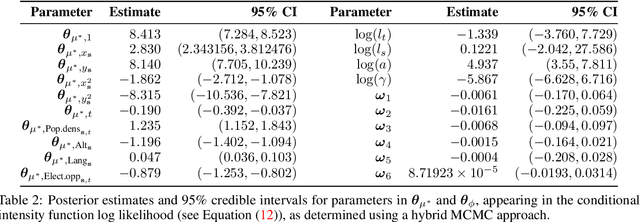
Extreme events with potential deadly outcomes, such as those organized by terror groups, are highly unpredictable in nature and an imminent threat to society. In particular, quantifying the likelihood of a terror attack occurring in an arbitrary space-time region and its relative societal risk, would facilitate informed measures that would strengthen national security. This paper introduces a novel self-exciting marked spatio-temporal model for attacks whose inhomogeneous baseline intensity is written as a function of covariates. Its triggering intensity is succinctly modeled with a Gaussian Process prior distribution to flexibly capture intricate spatio-temporal dependencies between an arbitrary attack and previous terror events. By inferring the parameters of this model, we highlight specific space-time areas in which attacks are likely to occur. Furthermore, by measuring the outcome of an attack in terms of the number of casualties it produces, we introduce a novel mixture distribution for the number of casualties. This distribution flexibly handles low and high number of casualties and the discrete nature of the data through a {\it Generalized ZipF} distribution. We rely on a customized Markov chain Monte Carlo (MCMC) method to estimate the model parameters. We illustrate the methodology with data from the open source Global Terrorism Database (GTD) that correspond to attacks in Afghanistan from 2013-2018. We show that our model is able to predict the intensity of future attacks for 2019-2021 while considering various covariates of interest such as population density, number of regional languages spoken, and the density of population supporting the opposing government.