Collaborative Low-Rank Subspace Clustering

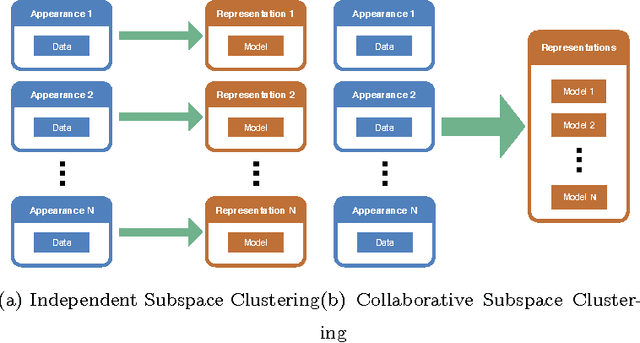
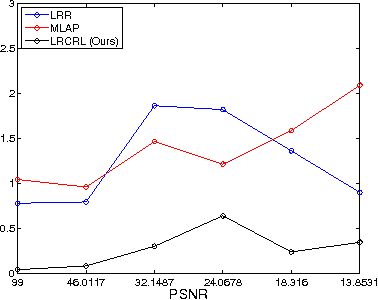
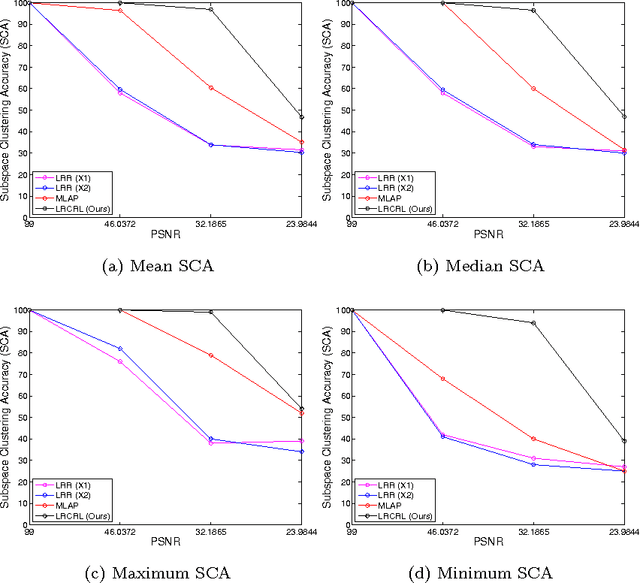
In this paper we present Collaborative Low-Rank Subspace Clustering. Given multiple observations of a phenomenon we learn a unified representation matrix. This unified matrix incorporates the features from all the observations, thus increasing the discriminative power compared with learning the representation matrix on each observation separately. Experimental evaluation shows that our method outperforms subspace clustering on separate observations and the state of the art collaborative learning algorithm.

Tractable Clustering of Data on the Curve Manifold

In machine learning it is common to interpret each data point as a vector in Euclidean space. However the data may actually be functional i.e.\ each data point is a function of some variable such as time and the function is discretely sampled. The naive treatment of functional data as traditional multivariate data can lead to poor performance since the algorithms are ignoring the correlation in the curvature of each function. In this paper we propose a tractable method to cluster functional data or curves by adapting the Euclidean Low-Rank Representation (LRR) to the curve manifold. Experimental evaluation on synthetic and real data reveals that this method massively outperforms prior clustering methods in both speed and accuracy when clustering functional data.

Efficient Sparse Subspace Clustering by Nearest Neighbour Filtering

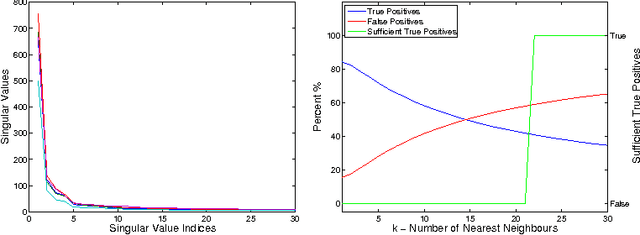
Sparse Subspace Clustering (SSC) has been used extensively for subspace identification tasks due to its theoretical guarantees and relative ease of implementation. However SSC has quadratic computation and memory requirements with respect to the number of input data points. This burden has prohibited SSCs use for all but the smallest datasets. To overcome this we propose a new method, k-SSC, that screens out a large number of data points to both reduce SSC to linear memory and computational requirements. We provide theoretical analysis for the bounds of success for k-SSC. Our experiments show that k-SSC exceeds theoretical expectations and outperforms existing SSC approximations by maintaining the classification performance of SSC. Furthermore in the spirit of reproducible research we have publicly released the source code for k-SSC

Low-Rank Representation over the Manifold of Curves

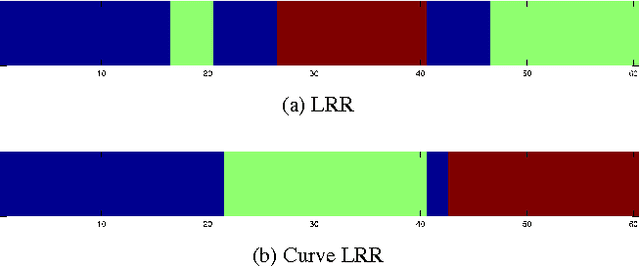
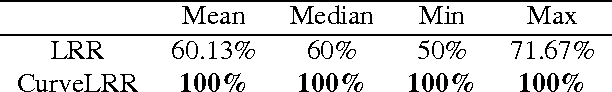
In machine learning it is common to interpret each data point as a vector in Euclidean space. However the data may actually be functional i.e.\ each data point is a function of some variable such as time and the function is discretely sampled. The naive treatment of functional data as traditional multivariate data can lead to poor performance since the algorithms are ignoring the correlation in the curvature of each function. In this paper we propose a method to analyse subspace structure of the functional data by using the state of the art Low-Rank Representation (LRR). Experimental evaluation on synthetic and real data reveals that this method massively outperforms conventional LRR in tasks concerning functional data.

Segmentation of Subspaces in Sequential Data

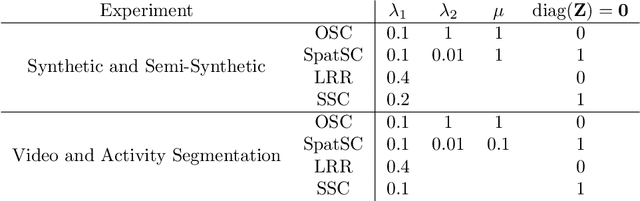
We propose Ordered Subspace Clustering (OSC) to segment data drawn from a sequentially ordered union of subspaces. Similar to Sparse Subspace Clustering (SSC) we formulate the problem as one of finding a sparse representation but include an additional penalty term to take care of sequential data. We test our method on data drawn from infrared hyper spectral, video and motion capture data. Experiments show that our method, OSC, outperforms the state of the art methods: Spatial Subspace Clustering (SpatSC), Low-Rank Representation (LRR) and SSC.