Rapid Whole Brain Mesoscale In-vivo MR Imaging using Multi-scale Implicit Neural Representation

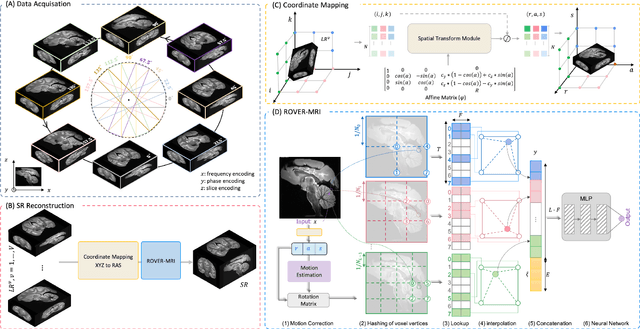
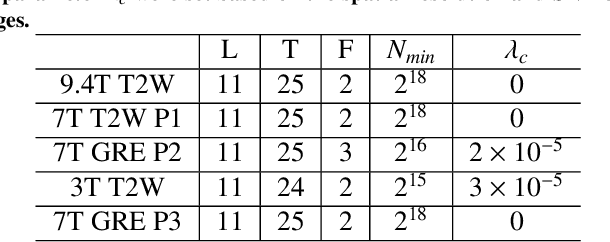
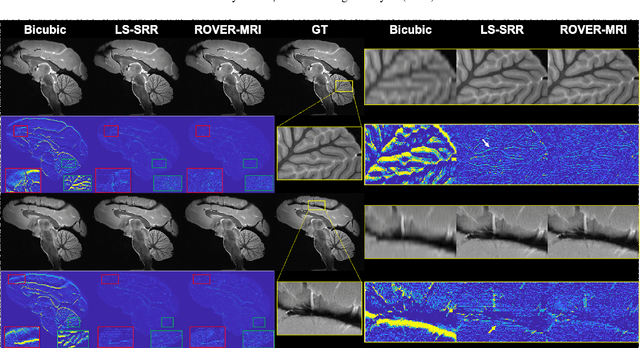
Purpose: To develop and validate a novel image reconstruction technique using implicit neural representations (INR) for multi-view thick-slice acquisitions while reducing the scan time but maintaining high signal-to-noise ratio (SNR). Methods: We propose Rotating-view super-resolution (ROVER)-MRI, an unsupervised neural network-based algorithm designed to reconstruct MRI data from multi-view thick slices, effectively reducing scan time by 2-fold while maintaining fine anatomical details. We compare our method to both bicubic interpolation and the current state-of-the-art regularized least-squares super-resolution reconstruction (LS-SRR) technique. Validation is performed using ground-truth ex-vivo monkey brain data, and we demonstrate superior reconstruction quality across several in-vivo human datasets. Notably, we achieve the reconstruction of a whole human brain in-vivo T2-weighted image with an unprecedented 180{\mu}m isotropic spatial resolution, accomplished in just 17 minutes of scan time on a 7T MRI scanner. Results: ROVER-MRI outperformed LS-SRR method in terms of reconstruction quality with 22.4% lower relative error (RE) and 7.5% lower full-width half maximum (FWHM) indicating better preservation of fine structural details in nearly half the scan time. Conclusion: ROVER-MRI offers an efficient and robust approach for mesoscale MR imaging, enabling rapid, high-resolution whole-brain scans. Its versatility holds great promise for research applications requiring anatomical details and time-efficient imaging.

NeuroPMD: Neural Fields for Density Estimation on Product Manifolds

We propose a novel deep neural network methodology for density estimation on product Riemannian manifold domains. In our approach, the network directly parameterizes the unknown density function and is trained using a penalized maximum likelihood framework, with a penalty term formed using manifold differential operators. The network architecture and estimation algorithm are carefully designed to handle the challenges of high-dimensional product manifold domains, effectively mitigating the curse of dimensionality that limits traditional kernel and basis expansion estimators, as well as overcoming the convergence issues encountered by non-specialized neural network methods. Extensive simulations and a real-world application to brain structural connectivity data highlight the clear advantages of our method over the competing alternatives.

Estimating Neural Orientation Distribution Fields on High Resolution Diffusion MRI Scans

The Orientation Distribution Function (ODF) characterizes key brain microstructural properties and plays an important role in understanding brain structural connectivity. Recent works introduced Implicit Neural Representation (INR) based approaches to form a spatially aware continuous estimate of the ODF field and demonstrated promising results in key tasks of interest when compared to conventional discrete approaches. However, traditional INR methods face difficulties when scaling to large-scale images, such as modern ultra-high-resolution MRI scans, posing challenges in learning fine structures as well as inefficiencies in training and inference speed. In this work, we propose HashEnc, a grid-hash-encoding-based estimation of the ODF field and demonstrate its effectiveness in retaining structural and textural features. We show that HashEnc achieves a 10% enhancement in image quality while requiring 3x less computational resources than current methods. Our code can be found at https://github.com/MunzerDw/NODF-HashEnc.

Neural Orientation Distribution Fields for Estimation and Uncertainty Quantification in Diffusion MRI

Inferring brain connectivity and structure \textit{in-vivo} requires accurate estimation of the orientation distribution function (ODF), which encodes key local tissue properties. However, estimating the ODF from diffusion MRI (dMRI) signals is a challenging inverse problem due to obstacles such as significant noise, high-dimensional parameter spaces, and sparse angular measurements. In this paper, we address these challenges by proposing a novel deep-learning based methodology for continuous estimation and uncertainty quantification of the spatially varying ODF field. We use a neural field (NF) to parameterize a random series representation of the latent ODFs, implicitly modeling the often ignored but valuable spatial correlation structures in the data, and thereby improving efficiency in sparse and noisy regimes. An analytic approximation to the posterior predictive distribution is derived which can be used to quantify the uncertainty in the ODF estimate at any spatial location, avoiding the need for expensive resampling-based approaches that are typically employed for this purpose. We present empirical evaluations on both synthetic and real in-vivo diffusion data, demonstrating the advantages of our method over existing approaches.

Efficient Multidimensional Functional Data Analysis Using Marginal Product Basis Systems

Modern datasets, from areas such as neuroimaging and geostatistics, often come in the form of a random sample of tensor-valued data which can be understood as noisy observations of an underlying smooth multidimensional random function. Many of the traditional techniques from functional data analysis are plagued by the curse of dimensionality and quickly become intractable as the dimension of the domain increases. In this paper, we propose a framework for learning multidimensional continuous representations from a random sample of tensors that is immune to several manifestations of the curse. These representations are defined to be multiplicatively separable and adapted to the data according to an $L^{2}$ optimality criteria, analogous to a multidimensional functional principal components analysis. We show that the resulting estimation problem can be solved efficiently by the tensor decomposition of a carefully defined reduction transformation of the observed data. The incorporation of both regularization and dimensionality reduction is discussed. The advantages of the proposed method over competing methods are demonstrated in a simulation study. We conclude with a real data application in neuroimaging.