Robust Flow-based Conformal Inference (FCI) with Statistical Guarantee

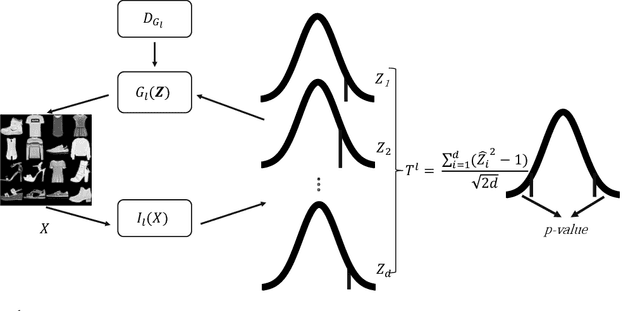
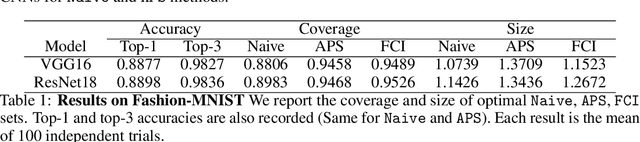
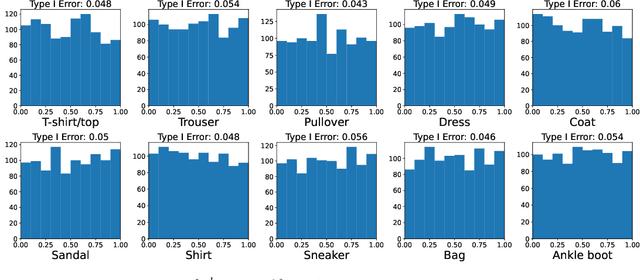
Conformal prediction aims to determine precise levels of confidence in predictions for new objects using past experience. However, the commonly used exchangeable assumptions between the training data and testing data limit its usage in dealing with contaminated testing sets. In this paper, we develop a series of conformal inference methods, including building predictive sets and inferring outliers for complex and high-dimensional data. We leverage ideas from adversarial flow to transfer the input data to a random vector with known distributions, which enable us to construct a non-conformity score for uncertainty quantification. We can further learn the distribution of input data in each class directly through the learned transformation. Therefore, our approach is applicable and more robust when the test data is contaminated. We evaluate our method, robust flow-based conformal inference, on benchmark datasets. We find that it produces effective prediction sets and accurate outlier detection and is more powerful relative to competing approaches.

DVE: Dynamic Variational Embeddings with Applications in Recommender Systems

Embedding is a useful technique to project a high-dimensional feature into a low-dimensional space, and it has many successful applications including link prediction, node classification and natural language processing. Current approaches mainly focus on static data, which usually lead to unsatisfactory performance in applications involving large changes over time. How to dynamically characterize the variation of the embedded features is still largely unexplored. In this paper, we introduce a dynamic variational embedding (DVE) approach for sequence-aware data based on recent advances in recurrent neural networks. DVE can model the node's intrinsic nature and temporal variation explicitly and simultaneously, which are crucial for exploration. We further apply DVE to sequence-aware recommender systems, and develop an end-to-end neural architecture for link prediction.

Variational Auto-encoder for Recommender Systems with Exploration-Exploitation

Variational auto-encoder (VAE) is an efficient non-linear latent factor model that has been widely applied in recommender systems (RS). However, a drawback of VAE for RS is their inability of exploration. A good RS is expected to recommend items that are known to enjoy and items that are novel to try. In this work, we introduce an exploitation-exploration motivated VAE (XploVAE) to collaborative filtering. To facilitate personalized recommendations, we construct user-specific subgraphs, which contain the first-order proximity capturing observed user-item interactions for exploitation and the higher-order proximity for exploration. We further develop a hierarchical latent space model to learn the population distribution of the user subgraphs, and learn the personalized item embedding. Empirical experiments prove the effectiveness of our proposed method on various real-world data sets.

Reproducible Bootstrap Aggregating

Heterogeneity between training and testing data degrades reproducibility of a well-trained predictive algorithm. In modern applications, how to deploy a trained algorithm in a different domain is becoming an urgent question raised by many domain scientists. In this paper, we propose a reproducible bootstrap aggregating (Rbagging) method coupled with a new algorithm, the iterative nearest neighbor sampler (INNs), effectively drawing bootstrap samples from training data to mimic the distribution of the test data. Rbagging is a general ensemble framework that can be applied to most classifiers. We further propose Rbagging+ to effectively detect anomalous samples in the testing data. Our theoretical results show that the resamples based on Rbagging have the same distribution as the testing data. Moreover, under suitable assumptions, we further provide a general bound to control the test excess risk of the ensemble classifiers. The proposed method is compared with several other popular domain adaptation methods via extensive simulation studies and real applications including medical diagnosis and imaging classifications.

Auto-encoding graph-valued data with applications to brain connectomes

Our interest focuses on developing statistical methods for analysis of brain structural connectomes. Nodes in the brain connectome graph correspond to different regions of interest (ROIs) while edges correspond to white matter fiber connections between these ROIs. Due to the high-dimensionality and non-Euclidean nature of the data, it becomes challenging to conduct analyses of the population distribution of brain connectomes and relate connectomes to other factors, such as cognition. Current approaches focus on summarizing the graph using either pre-specified topological features or principal components analysis (PCA). In this article, we instead develop a nonlinear latent factor model for summarizing the brain graph in both unsupervised and supervised settings. The proposed approach builds on methods for hierarchical modeling of replicated graph data, as well as variational auto-encoders that use neural networks for dimensionality reduction. We refer to our method as Graph AuTo-Encoding (GATE). We compare GATE with tensor PCA and other competitors through simulations and applications to data from the Human Connectome Project (HCP).

Early Stopping for Nonparametric Testing

Early stopping of iterative algorithms is an algorithmic regularization method to avoid over-fitting in estimation and classification. In this paper, we show that early stopping can also be applied to obtain the minimax optimal testing in a general non-parametric setup. Specifically, a Wald-type test statistic is obtained based on an iterated estimate produced by functional gradient descent algorithms in a reproducing kernel Hilbert space. A notable contribution is to establish a "sharp" stopping rule: when the number of iterations achieves an optimal order, testing optimality is achievable; otherwise, testing optimality becomes impossible. As a by-product, a similar sharpness result is also derived for minimax optimal estimation under early stopping studied in [11] and [19]. All obtained results hold for various kernel classes, including Sobolev smoothness classes and Gaussian kernel classes.

How Many Machines Can We Use in Parallel Computing for Kernel Ridge Regression?

This paper attempts to solve a basic problem in distributed statistical inference: how many machines can we use in parallel computing? In kernel ridge regression, we address this question in two important settings: nonparametric estimation and hypothesis testing. Specifically, we find a range for the number of machines under which optimal estimation/testing is achievable. The employed empirical processes method provides a unified framework, that allows us to handle various regression problems (such as thin-plate splines and nonparametric additive regression) under different settings (such as univariate, multivariate and diverging-dimensional designs). It is worth noting that the upper bounds of the number of machines are proven to be un-improvable (up to a logarithmic factor) in two important cases: smoothing spline regression and Gaussian RKHS regression. Our theoretical findings are backed by thorough numerical studies.

Statistically and Computationally Efficient Variance Estimator for Kernel Ridge Regression

In this paper, we propose a random projection approach to estimate variance in kernel ridge regression. Our approach leads to a consistent estimator of the true variance, while being computationally more efficient. Our variance estimator is optimal for a large family of kernels, including cubic splines and Gaussian kernels. Simulation analysis is conducted to support our theory.

Nonparametric Testing under Random Projection

A common challenge in nonparametric inference is its high computational complexity when data volume is large. In this paper, we develop computationally efficient nonparametric testing by employing a random projection strategy. In the specific kernel ridge regression setup, a simple distance-based test statistic is proposed. Notably, we derive the minimum number of random projections that is sufficient for achieving testing optimality in terms of the minimax rate. An adaptive testing procedure is further established without prior knowledge of regularity. One technical contribution is to establish upper bounds for a range of tail sums of empirical kernel eigenvalues. Simulations and real data analysis are conducted to support our theory.