Statistical Inference with Stochastic Gradient Methods under $φ$-mixing Data

Stochastic gradient descent (SGD) is a scalable and memory-efficient optimization algorithm for large datasets and stream data, which has drawn a great deal of attention and popularity. The applications of SGD-based estimators to statistical inference such as interval estimation have also achieved great success. However, most of the related works are based on i.i.d. observations or Markov chains. When the observations come from a mixing time series, how to conduct valid statistical inference remains unexplored. As a matter of fact, the general correlation among observations imposes a challenge on interval estimation. Most existing methods may ignore this correlation and lead to invalid confidence intervals. In this paper, we propose a mini-batch SGD estimator for statistical inference when the data is $\phi$-mixing. The confidence intervals are constructed using an associated mini-batch bootstrap SGD procedure. Using ``independent block'' trick from \cite{yu1994rates}, we show that the proposed estimator is asymptotically normal, and its limiting distribution can be effectively approximated by the bootstrap procedure. The proposed method is memory-efficient and easy to implement in practice. Simulation studies on synthetic data and an application to a real-world dataset confirm our theory.

Solar Flare Index Prediction Using SDO/HMI Vector Magnetic Data Products with Statistical and Machine Learning Methods

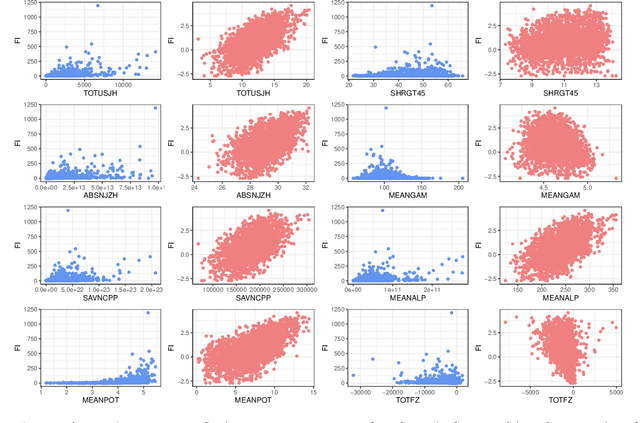
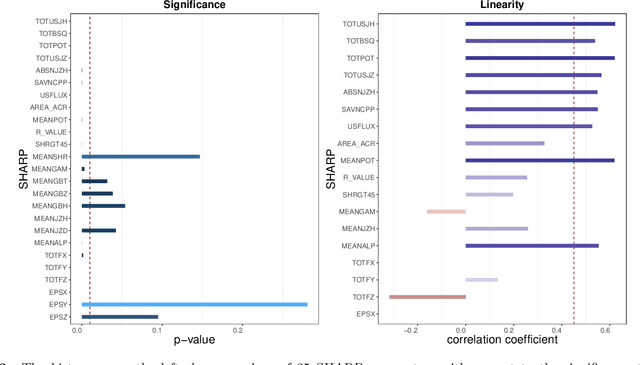
Solar flares, especially the M- and X-class flares, are often associated with coronal mass ejections (CMEs). They are the most important sources of space weather effects, that can severely impact the near-Earth environment. Thus it is essential to forecast flares (especially the M-and X-class ones) to mitigate their destructive and hazardous consequences. Here, we introduce several statistical and Machine Learning approaches to the prediction of the AR's Flare Index (FI) that quantifies the flare productivity of an AR by taking into account the numbers of different class flares within a certain time interval. Specifically, our sample includes 563 ARs appeared on solar disk from May 2010 to Dec 2017. The 25 magnetic parameters, provided by the Space-weather HMI Active Region Patches (SHARP) from Helioseismic and Magnetic Imager (HMI) on board the Solar Dynamics Observatory (SDO), characterize coronal magnetic energy stored in ARs by proxy and are used as the predictors. We investigate the relationship between these SHARP parameters and the FI of ARs with a machine-learning algorithm (spline regression) and the resampling method (Synthetic Minority Over-Sampling Technique for Regression with Gaussian Noise, short by SMOGN). Based on the established relationship, we are able to predict the value of FIs for a given AR within the next 1-day period. Compared with other 4 popular machine learning algorithms, our methods improve the accuracy of FI prediction, especially for large FI. In addition, we sort the importance of SHARP parameters by Borda Count method calculated from the ranks that are rendered by 9 different machine learning methods.

Deep Neural Network Classifier for Multi-dimensional Functional Data

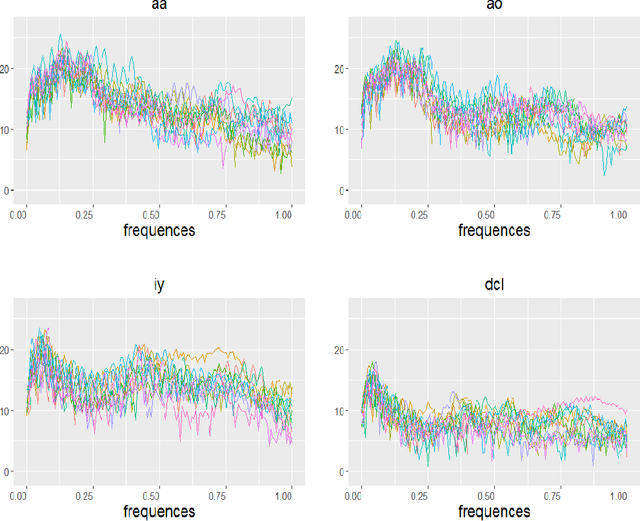
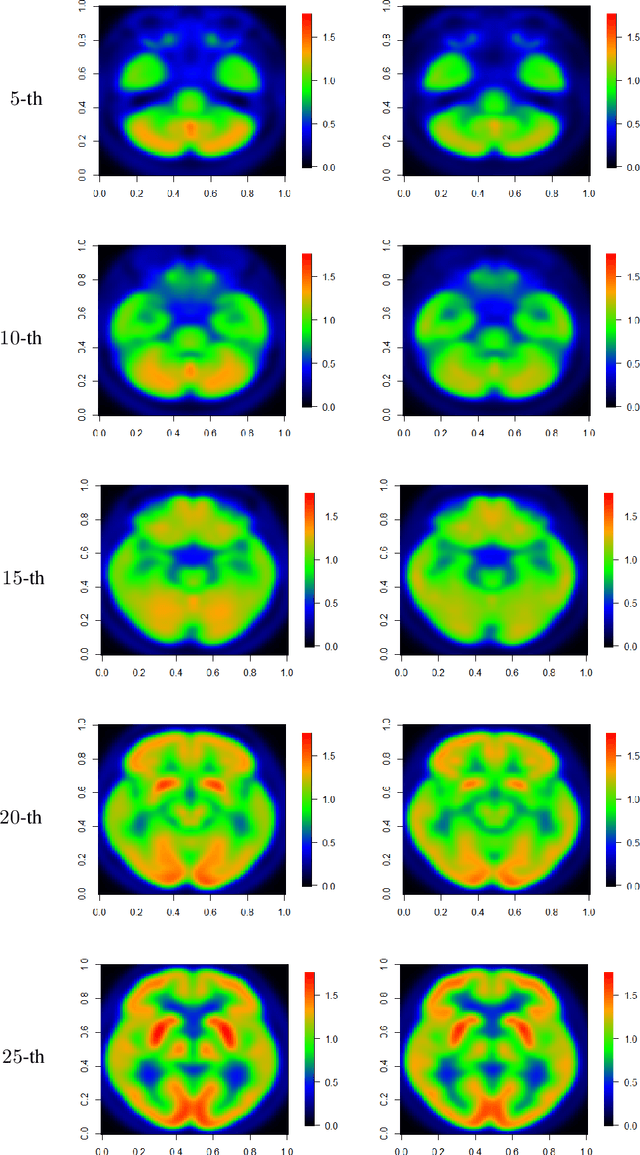
We propose a new approach, called as functional deep neural network (FDNN), for classifying multi-dimensional functional data. Specifically, a deep neural network is trained based on the principle components of the training data which shall be used to predict the class label of a future data function. Unlike the popular functional discriminant analysis approaches which rely on Gaussian assumption, the proposed FDNN approach applies to general non-Gaussian multi-dimensional functional data. Moreover, when the log density ratio possesses a locally connected functional modular structure, we show that FDNN achieves minimax optimality. The superiority of our approach is demonstrated through both simulated and real-world datasets.

Statistical Limits for Testing Correlation of Hypergraphs

In this paper, we consider the hypothesis testing of correlation between two $m$-uniform hypergraphs on $n$ unlabelled nodes. Under the null hypothesis, the hypergraphs are independent, while under the alternative hypothesis, the hyperdges have the same marginal distributions as in the null hypothesis but are correlated after some unknown node permutation. We focus on two scenarios: the hypergraphs are generated from the Gaussian-Wigner model and the dense Erd\"{o}s-R\'{e}nyi model. We derive the sharp information-theoretic testing threshold. Above the threshold, there exists a powerful test to distinguish the alternative hypothesis from the null hypothesis. Below the threshold, the alternative hypothesis and the null hypothesis are not distinguishable. The threshold involves $m$ and decreases as $m$ gets larger. This indicates testing correlation of hypergraphs ($m\geq3$) becomes easier than testing correlation of graphs ($m=2$)

Calibrating multi-dimensional complex ODE from noisy data via deep neural networks

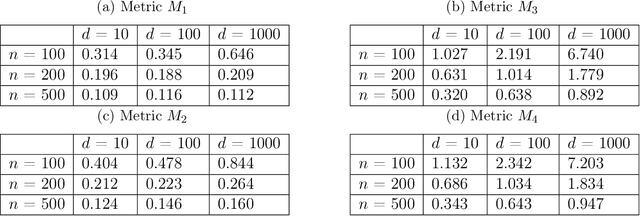
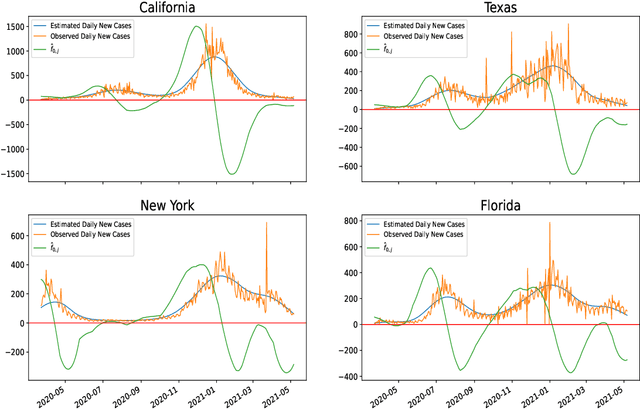
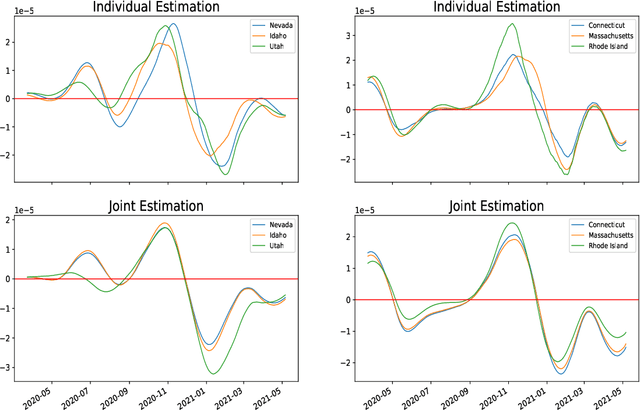
Ordinary differential equations (ODEs) are widely used to model complex dynamics that arises in biology, chemistry, engineering, finance, physics, etc. Calibration of a complicated ODE system using noisy data is generally very difficult. In this work, we propose a two-stage nonparametric approach to address this problem. We first extract the de-noised data and their higher order derivatives using boundary kernel method, and then feed them into a sparsely connected deep neural network with ReLU activation function. Our method is able to recover the ODE system without being subject to the curse of dimensionality and complicated ODE structure. When the ODE possesses a general modular structure, with each modular component involving only a few input variables, and the network architecture is properly chosen, our method is proven to be consistent. Theoretical properties are corroborated by an extensive simulation study that demonstrates the validity and effectiveness of the proposed method. Finally, we use our method to simultaneously characterize the growth rate of Covid-19 infection cases from 50 states of the USA.

Online Statistical Inference for Parameters Estimation with Linear-Equality Constraints

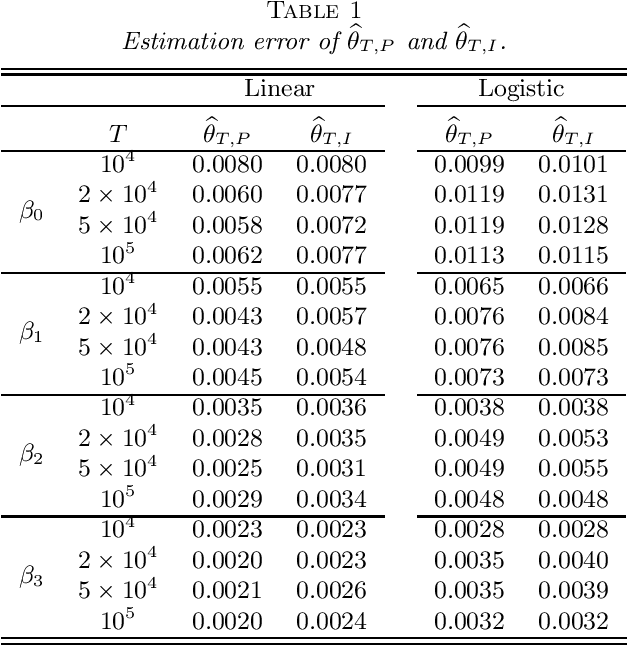
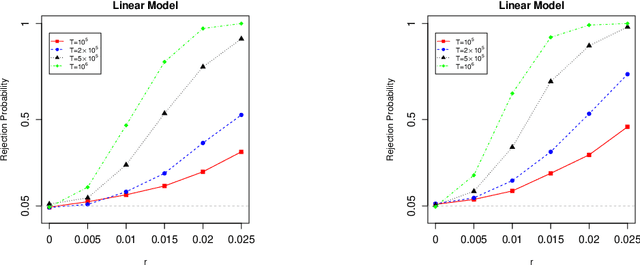
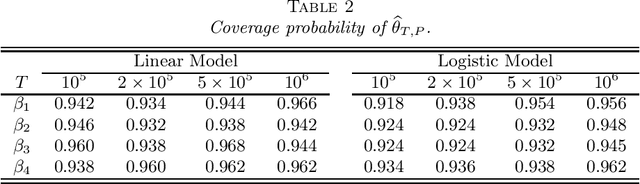
Stochastic gradient descent (SGD) and projected stochastic gradient descent (PSGD) are scalable algorithms to compute model parameters in unconstrained and constrained optimization problems. In comparison with stochastic gradient descent (SGD), PSGD forces its iterative values into the constrained parameter space via projection. The convergence rate of PSGD-type estimates has been exhaustedly studied, while statistical properties such as asymptotic distribution remain less explored. From a purely statistical point of view, this paper studies the limiting distribution of PSGD-based estimate when the true parameters satisfying some linear-equality constraints. Our theoretical findings reveal the role of projection played in the uncertainty of the PSGD estimate. As a byproduct, we propose an online hypothesis testing procedure to test the linear-equality constraints. Simulation studies on synthetic data and an application to a real-world dataset confirm our theory.

Distributed Adaptive Nearest Neighbor Classifier: Algorithm and Theory

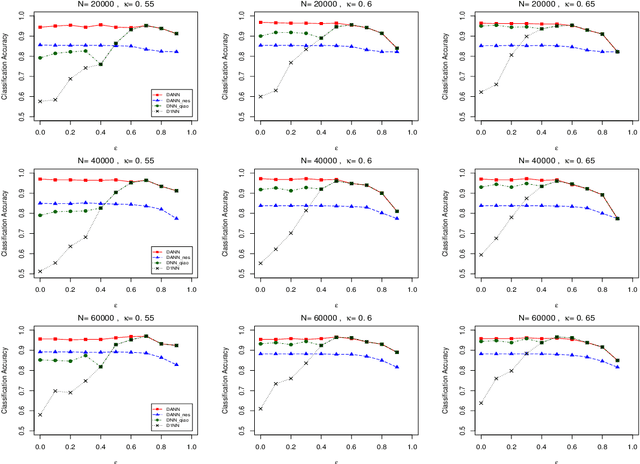
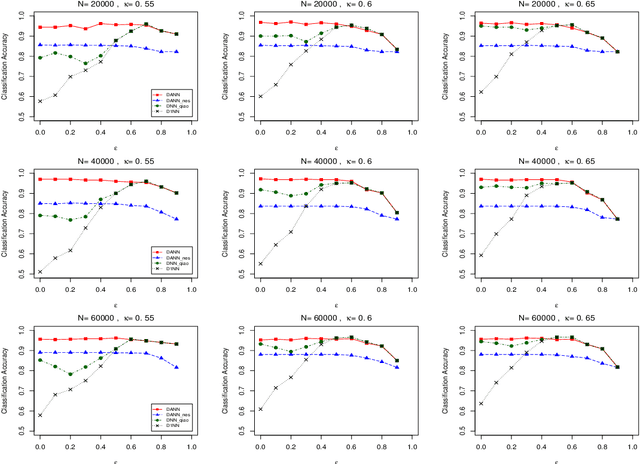
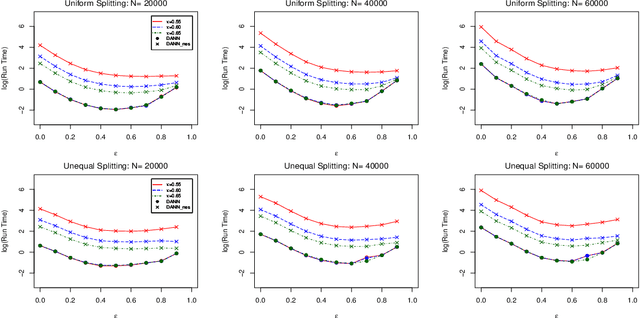
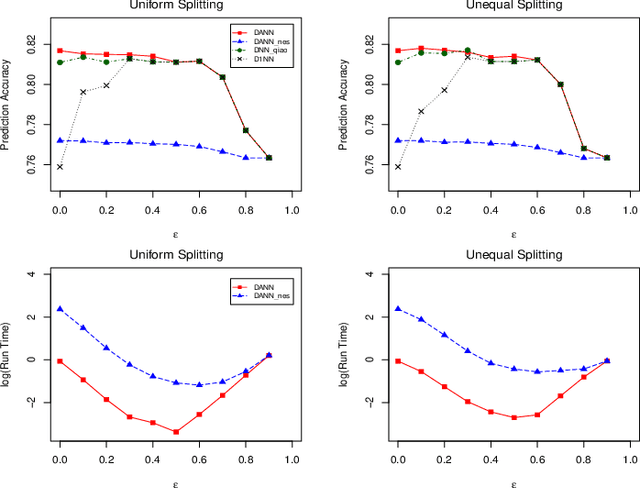
When data is of an extraordinarily large size or physically stored in different locations, the distributed nearest neighbor (NN) classifier is an attractive tool for classification. We propose a novel distributed adaptive NN classifier for which the number of nearest neighbors is a tuning parameter stochastically chosen by a data-driven criterion. An early stopping rule is proposed when searching for the optimal tuning parameter, which not only speeds up the computation but also improves the finite sample performance of the proposed Algorithm. Convergence rate of excess risk of the distributed adaptive NN classifier is investigated under various sub-sample size compositions. In particular, we show that when the sub-sample sizes are sufficiently large, the proposed classifier achieves the nearly optimal convergence rate. Effectiveness of the proposed approach is demonstrated through simulation studies as well as an empirical application to a real-world dataset.

Information Limits for Detecting a Subhypergraph

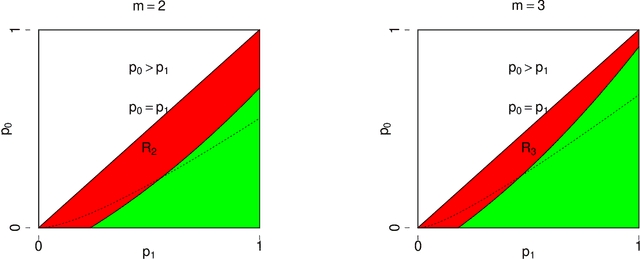
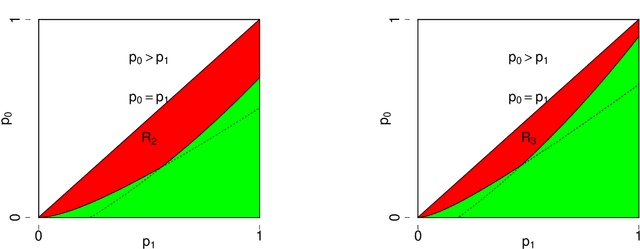
We consider the problem of recovering a subhypergraph based on an observed adjacency tensor corresponding to a uniform hypergraph. The uniform hypergraph is assumed to contain a subset of vertices called as subhypergraph. The edges restricted to the subhypergraph are assumed to follow a different probability distribution than other edges. We consider both weak recovery and exact recovery of the subhypergraph, and establish information-theoretic limits in each case. Specifically, we establish sharp conditions for the possibility of weakly or exactly recovering the subhypergraph from an information-theoretic point of view. These conditions are fundamentally different from their counterparts derived in hypothesis testing literature.

Heterogeneous Dense Subhypergraph Detection

We study the problem of testing the existence of a heterogeneous dense subhypergraph. The null hypothesis corresponds to a heterogeneous Erd\"{o}s-R\'{e}nyi uniform random hypergraph and the alternative hypothesis corresponds to a heterogeneous uniform random hypergraph that contains a dense subhypergraph. We establish detection boundaries when the edge probabilities are known and construct an asymptotically powerful test for distinguishing the hypotheses. We also construct an adaptive test which does not involve edge probabilities, and hence, is more practically useful.

Sharp detection boundaries on testing dense subhypergraph

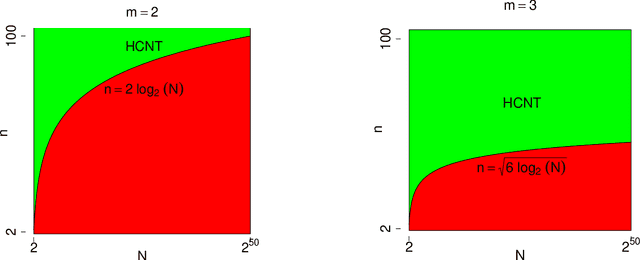
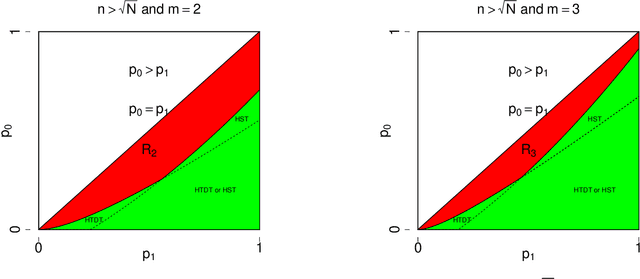
We study the problem of testing the existence of a dense subhypergraph. The null hypothesis is an Erdos-Renyi uniform random hypergraph and the alternative hypothesis is a uniform random hypergraph that contains a dense subhypergraph. We establish sharp detection boundaries in both scenarios: (1) the edge probabilities are known; (2) the edge probabilities are unknown. In both scenarios, sharp detectable boundaries are characterized by the appropriate model parameters. Asymptotically powerful tests are provided when the model parameters fall in the detectable regions. Our results indicate that the detectable regions for general hypergraph models are dramatically different from their graph counterparts.