Online Statistical Inference for Parameters Estimation with Linear-Equality Constraints
Paper and Code
May 21, 2021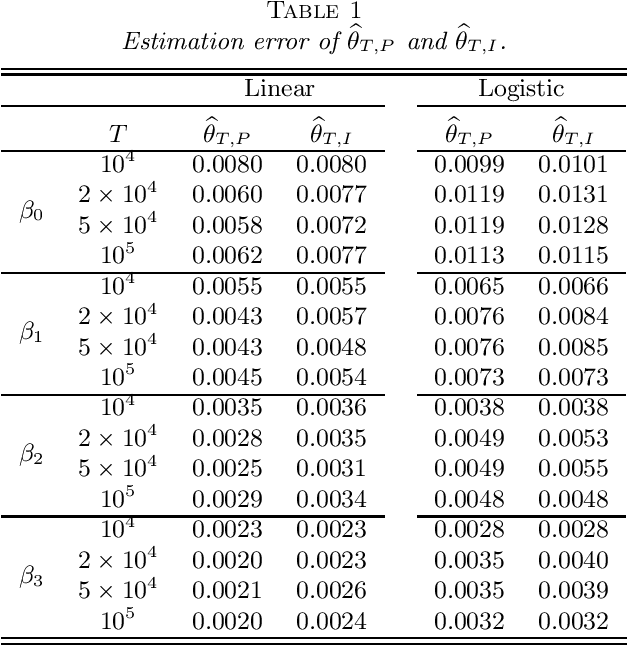
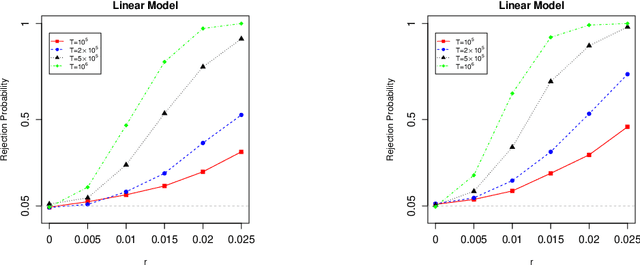
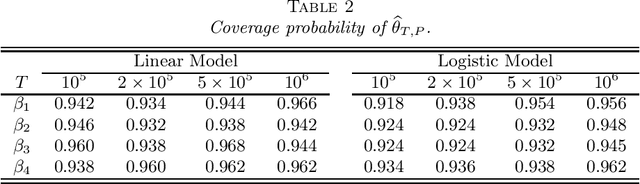
Stochastic gradient descent (SGD) and projected stochastic gradient descent (PSGD) are scalable algorithms to compute model parameters in unconstrained and constrained optimization problems. In comparison with stochastic gradient descent (SGD), PSGD forces its iterative values into the constrained parameter space via projection. The convergence rate of PSGD-type estimates has been exhaustedly studied, while statistical properties such as asymptotic distribution remain less explored. From a purely statistical point of view, this paper studies the limiting distribution of PSGD-based estimate when the true parameters satisfying some linear-equality constraints. Our theoretical findings reveal the role of projection played in the uncertainty of the PSGD estimate. As a byproduct, we propose an online hypothesis testing procedure to test the linear-equality constraints. Simulation studies on synthetic data and an application to a real-world dataset confirm our theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge