Statistical Limits for Testing Correlation of Hypergraphs

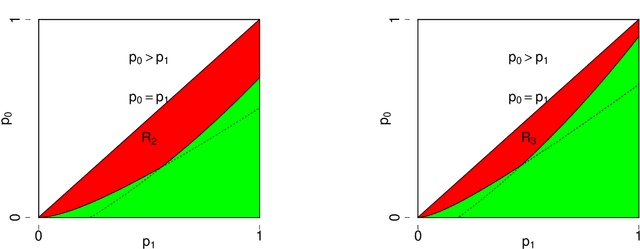
In this paper, we consider the hypothesis testing of correlation between two $m$-uniform hypergraphs on $n$ unlabelled nodes. Under the null hypothesis, the hypergraphs are independent, while under the alternative hypothesis, the hyperdges have the same marginal distributions as in the null hypothesis but are correlated after some unknown node permutation. We focus on two scenarios: the hypergraphs are generated from the Gaussian-Wigner model and the dense Erd\"{o}s-R\'{e}nyi model. We derive the sharp information-theoretic testing threshold. Above the threshold, there exists a powerful test to distinguish the alternative hypothesis from the null hypothesis. Below the threshold, the alternative hypothesis and the null hypothesis are not distinguishable. The threshold involves $m$ and decreases as $m$ gets larger. This indicates testing correlation of hypergraphs ($m\geq3$) becomes easier than testing correlation of graphs ($m=2$)

Community detection in censored hypergraph

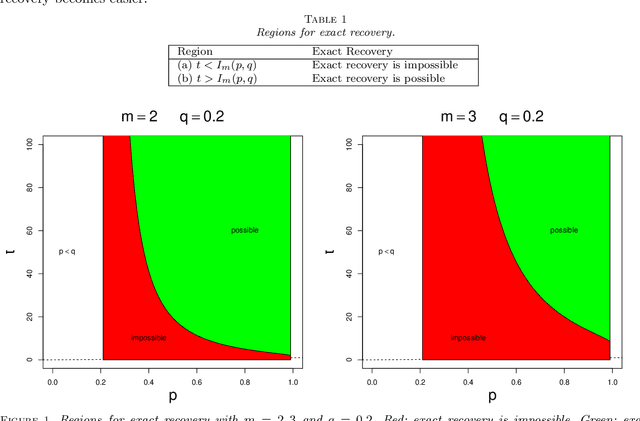
Community detection refers to the problem of clustering the nodes of a network (either graph or hypergrah) into groups. Various algorithms are available for community detection and all these methods apply to uncensored networks. In practice, a network may has censored (or missing) values and it is shown that censored values have non-negligible effect on the structural properties of a network. In this paper, we study community detection in censored $m$-uniform hypergraph from information-theoretic point of view. We derive the information-theoretic threshold for exact recovery of the community structure. Besides, we propose a polynomial-time algorithm to exactly recover the community structure up to the threshold. The proposed algorithm consists of a spectral algorithm plus a refinement step. It is also interesting to study whether a single spectral algorithm without refinement achieves the threshold. To this end, we also explore the semi-definite relaxation algorithm and analyze its performance.

Online Statistical Inference for Parameters Estimation with Linear-Equality Constraints

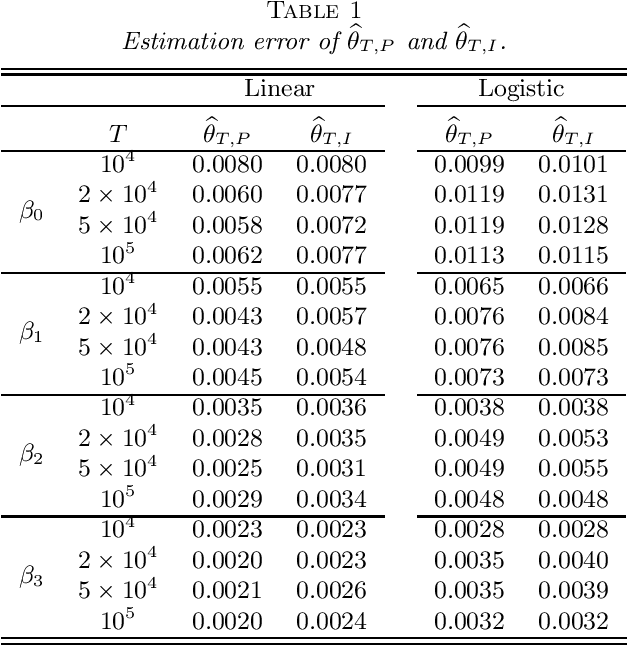
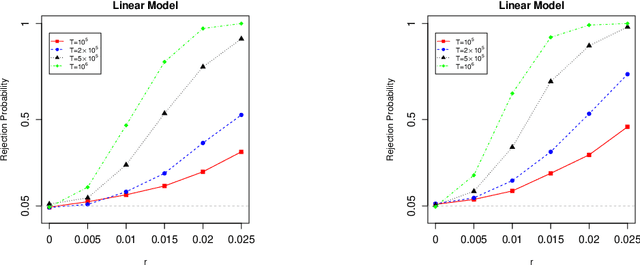
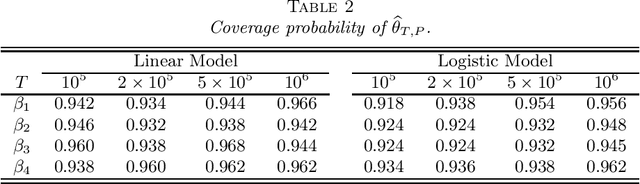
Stochastic gradient descent (SGD) and projected stochastic gradient descent (PSGD) are scalable algorithms to compute model parameters in unconstrained and constrained optimization problems. In comparison with stochastic gradient descent (SGD), PSGD forces its iterative values into the constrained parameter space via projection. The convergence rate of PSGD-type estimates has been exhaustedly studied, while statistical properties such as asymptotic distribution remain less explored. From a purely statistical point of view, this paper studies the limiting distribution of PSGD-based estimate when the true parameters satisfying some linear-equality constraints. Our theoretical findings reveal the role of projection played in the uncertainty of the PSGD estimate. As a byproduct, we propose an online hypothesis testing procedure to test the linear-equality constraints. Simulation studies on synthetic data and an application to a real-world dataset confirm our theory.

Information Limits for Detecting a Subhypergraph

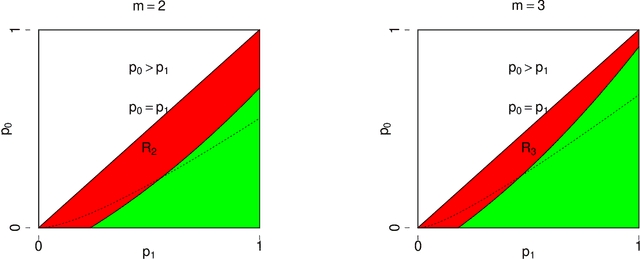
We consider the problem of recovering a subhypergraph based on an observed adjacency tensor corresponding to a uniform hypergraph. The uniform hypergraph is assumed to contain a subset of vertices called as subhypergraph. The edges restricted to the subhypergraph are assumed to follow a different probability distribution than other edges. We consider both weak recovery and exact recovery of the subhypergraph, and establish information-theoretic limits in each case. Specifically, we establish sharp conditions for the possibility of weakly or exactly recovering the subhypergraph from an information-theoretic point of view. These conditions are fundamentally different from their counterparts derived in hypothesis testing literature.

Heterogeneous Dense Subhypergraph Detection

We study the problem of testing the existence of a heterogeneous dense subhypergraph. The null hypothesis corresponds to a heterogeneous Erd\"{o}s-R\'{e}nyi uniform random hypergraph and the alternative hypothesis corresponds to a heterogeneous uniform random hypergraph that contains a dense subhypergraph. We establish detection boundaries when the edge probabilities are known and construct an asymptotically powerful test for distinguishing the hypotheses. We also construct an adaptive test which does not involve edge probabilities, and hence, is more practically useful.

A practical test for a planted community in heterogeneous networks

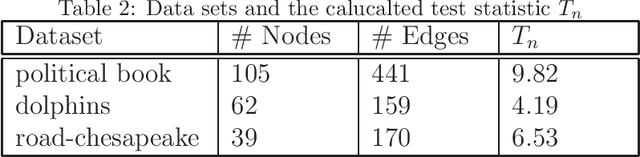
One of the fundamental task in graph data mining is to find a planted community(dense subgraph), which has wide application in biology, finance, spam detection and so on. For a real network data, the existence of a dense subgraph is generally unknown. Statistical tests have been devised to testing the existence of dense subgraph in a homogeneous random graph. However, many networks present extreme heterogeneity, that is, the degrees of nodes or vertexes don't concentrate on a typical value. The existing tests designed for homogeneous random graph are not straightforwardly applicable to the heterogeneous case. Recently, scan test was proposed for detecting a dense subgraph in heterogeneous(inhomogeneous) graph(\cite{BCHV19}). However, the computational complexity of the scan test is generally not polynomial in the graph size, which makes the test impractical for large or moderate networks. In this paper, we propose a polynomial-time test that has the standard normal distribution as the null limiting distribution. The power of the test is theoretically investigated and we evaluate the performance of the test by simulation and real data example.

Sharp detection boundaries on testing dense subhypergraph

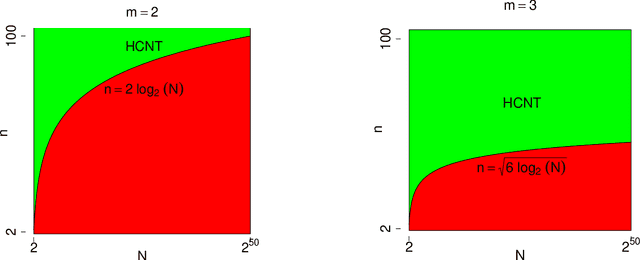
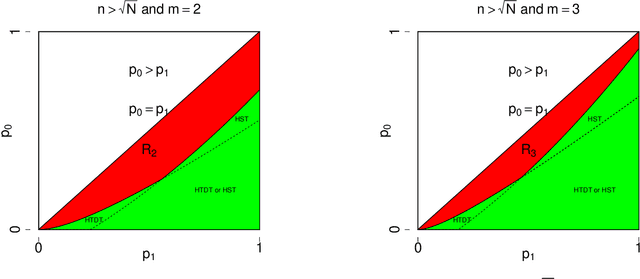
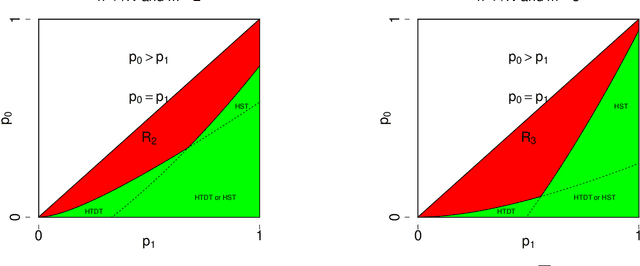
We study the problem of testing the existence of a dense subhypergraph. The null hypothesis is an Erdos-Renyi uniform random hypergraph and the alternative hypothesis is a uniform random hypergraph that contains a dense subhypergraph. We establish sharp detection boundaries in both scenarios: (1) the edge probabilities are known; (2) the edge probabilities are unknown. In both scenarios, sharp detectable boundaries are characterized by the appropriate model parameters. Asymptotically powerful tests are provided when the model parameters fall in the detectable regions. Our results indicate that the detectable regions for general hypergraph models are dramatically different from their graph counterparts.

A likelihood-ratio type test for stochastic block models with bounded degrees

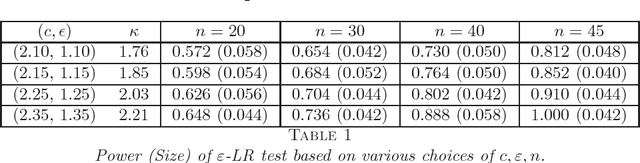
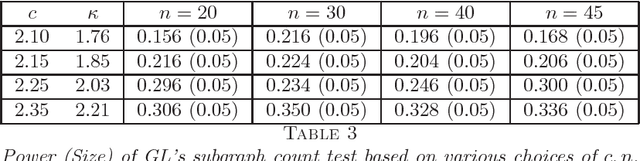
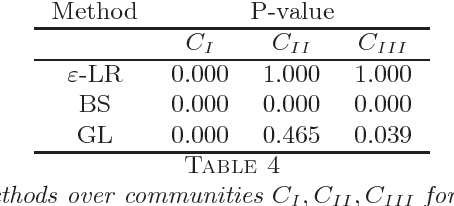
A fundamental problem in network data analysis is to test Erd\"{o}s-R\'{e}nyi model $\mathcal{G}\left(n,\frac{a+b}{2n}\right)$ versus a bisection stochastic block model $\mathcal{G}\left(n,\frac{a}{n},\frac{b}{n}\right)$, where $a,b>0$ are constants that represent the expected degrees of the graphs and $n$ denotes the number of nodes. This problem serves as the foundation of many other problems such as testing-based methods for determining the number of communities (\cite{BS16,L16}) and community detection (\cite{MS16}). Existing work has been focusing on growing-degree regime $a,b\to\infty$ (\cite{BS16,L16,MS16,BM17,B18,GL17a,GL17b}) while leaving the bounded-degree regime untreated. In this paper, we propose a likelihood-ratio (LR) type procedure based on regularization to test stochastic block models with bounded degrees. We derive the limit distributions as power Poisson laws under both null and alternative hypotheses, based on which the limit power of the test is carefully analyzed. We also examine a Monte-Carlo method that partly resolves the computational cost issue. The proposed procedures are examined by both simulated and real-world data. The proof depends on a contiguity theory developed by Janson \cite{J95}.