Sharp detection boundaries on testing dense subhypergraph
Paper and Code
Jan 12, 2021
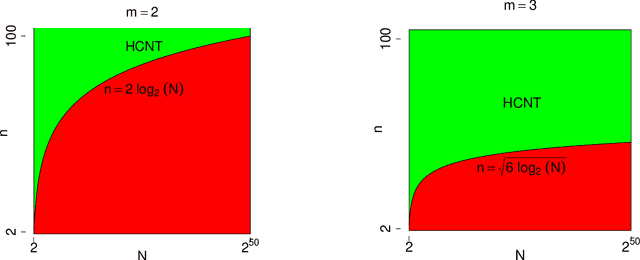
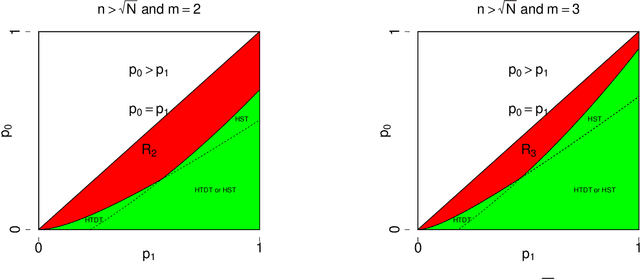
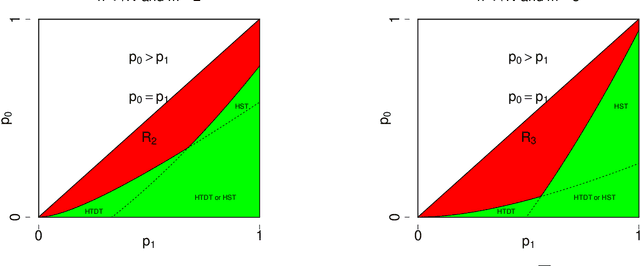
We study the problem of testing the existence of a dense subhypergraph. The null hypothesis is an Erdos-Renyi uniform random hypergraph and the alternative hypothesis is a uniform random hypergraph that contains a dense subhypergraph. We establish sharp detection boundaries in both scenarios: (1) the edge probabilities are known; (2) the edge probabilities are unknown. In both scenarios, sharp detectable boundaries are characterized by the appropriate model parameters. Asymptotically powerful tests are provided when the model parameters fall in the detectable regions. Our results indicate that the detectable regions for general hypergraph models are dramatically different from their graph counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge