Community detection in censored hypergraph
Paper and Code
Nov 04, 2021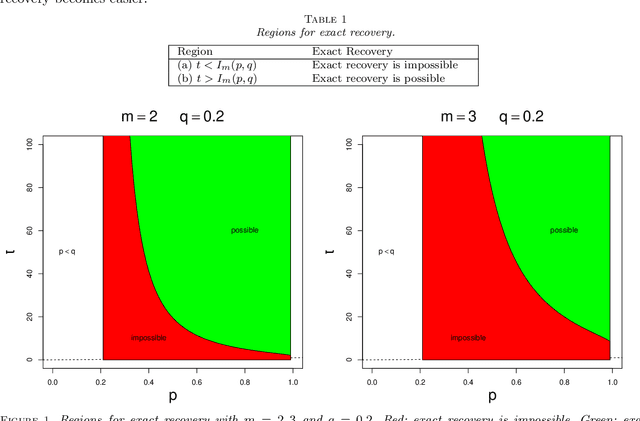
Community detection refers to the problem of clustering the nodes of a network (either graph or hypergrah) into groups. Various algorithms are available for community detection and all these methods apply to uncensored networks. In practice, a network may has censored (or missing) values and it is shown that censored values have non-negligible effect on the structural properties of a network. In this paper, we study community detection in censored $m$-uniform hypergraph from information-theoretic point of view. We derive the information-theoretic threshold for exact recovery of the community structure. Besides, we propose a polynomial-time algorithm to exactly recover the community structure up to the threshold. The proposed algorithm consists of a spectral algorithm plus a refinement step. It is also interesting to study whether a single spectral algorithm without refinement achieves the threshold. To this end, we also explore the semi-definite relaxation algorithm and analyze its performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge