Gradient is All You Need: Gradient-Based Attention Fusion for Infrared Small Target Detection

Infrared small target detection (IRSTD) is widely used in civilian and military applications. However, IRSTD encounters several challenges, including the tendency for small and dim targets to be obscured by complex backgrounds. To address this issue, we propose the Gradient Network (GaNet), which aims to extract and preserve edge and gradient information of small targets. GaNet employs the Gradient Transformer (GradFormer) module, simulating central difference convolutions (CDC) to extract and integrate gradient features with deeper features. Furthermore, we propose a global feature extraction model (GFEM) that offers a comprehensive perspective to prevent the network from focusing solely on details while neglecting the background information. We compare the network with state-of-the-art (SOTA) approaches, and the results demonstrate that our method performs effectively. Our source code is available at https://github.com/greekinRoma/Gradient-Transformer.

Deep Learning for Efficient GWAS Feature Selection

Genome-Wide Association Studies (GWAS) face unique challenges in the era of big genomics data, particularly when dealing with ultra-high-dimensional datasets where the number of genetic features significantly exceeds the available samples. This paper introduces an extension to the feature selection methodology proposed by Mirzaei et al. (2020), specifically tailored to tackle the intricacies associated with ultra-high-dimensional GWAS data. Our extended approach enhances the original method by introducing a Frobenius norm penalty into the student network, augmenting its capacity to adapt to scenarios characterized by a multitude of features and limited samples. Operating seamlessly in both supervised and unsupervised settings, our method employs two key neural networks. The first leverages an autoencoder or supervised autoencoder for dimension reduction, extracting salient features from the ultra-high-dimensional genomic data. The second network, a regularized feed-forward model with a single hidden layer, is designed for precise feature selection. The introduction of the Frobenius norm penalty in the student network significantly boosts the method's resilience to the challenges posed by ultra-high-dimensional GWAS datasets. Experimental results showcase the efficacy of our approach in feature selection for GWAS data. The method not only handles the inherent complexities of ultra-high-dimensional settings but also demonstrates superior adaptability to the nuanced structures present in genomics data. The flexibility and versatility of our proposed methodology are underscored by its successful performance across a spectrum of experiments.

On the Confidence Intervals in Bioequivalence Studies

A bioequivalence study is a type of clinical trial designed to compare the biological equivalence of two different formulations of a drug. Such studies are typically conducted in controlled clinical settings with human subjects, who are randomly assigned to receive two formulations. The two formulations are then compared with respect to their pharmacokinetic profiles, which encompass the absorption, distribution, metabolism, and elimination of the drug. Under the guidance from Food and Drug Administration (FDA), for a size-$\alpha$ bioequivalence test, the standard approach is to construct a $100(1-2\alpha)\%$ confidence interval and verify if the confidence interval falls with the critical region. In this work, we clarify that $100(1-2\alpha)\%$ confidence interval approach for bioequivalence testing yields a size-$\alpha$ test only when the two one-sided tests in TOST are ``equal-tailed''. Furthermore, a $100(1-\alpha)\%$ confidence interval approach is also discussed in the bioequivalence study.

Semiparametric Regression for Spatial Data via Deep Learning

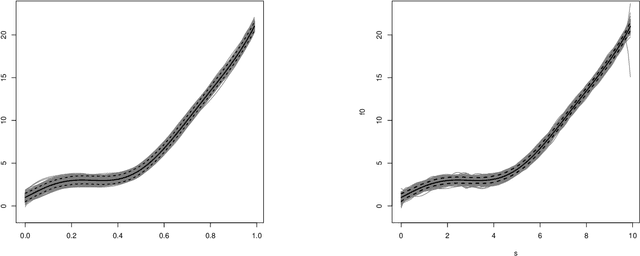
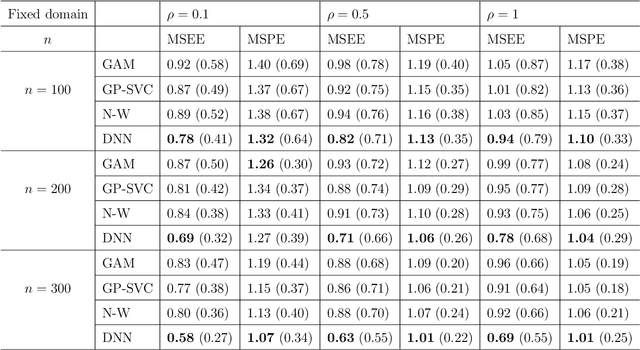
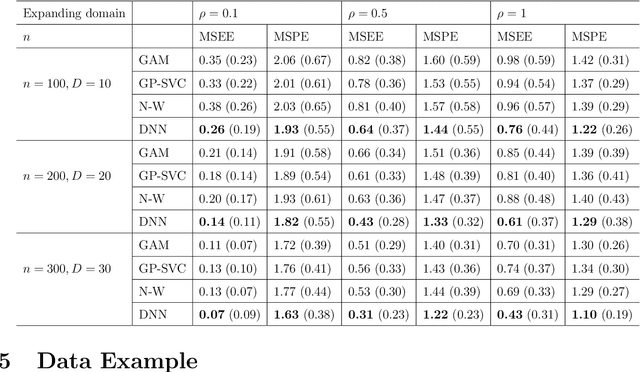
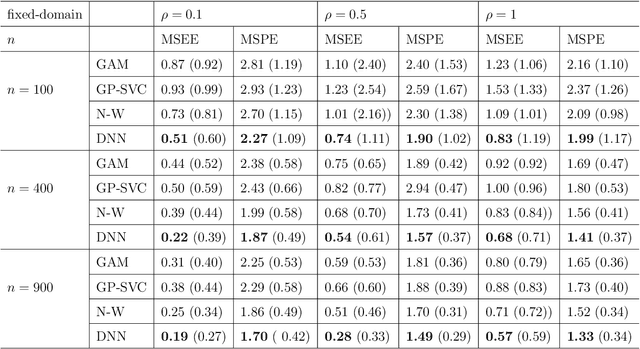
In this work, we propose a deep learning-based method to perform semiparametric regression analysis for spatially dependent data. To be specific, we use a sparsely connected deep neural network with rectified linear unit (ReLU) activation function to estimate the unknown regression function that describes the relationship between response and covariates in the presence of spatial dependence. Under some mild conditions, the estimator is proven to be consistent, and the rate of convergence is determined by three factors: (1) the architecture of neural network class, (2) the smoothness and (intrinsic) dimension of true mean function, and (3) the magnitude of spatial dependence. Our method can handle well large data set owing to the stochastic gradient descent optimization algorithm. Simulation studies on synthetic data are conducted to assess the finite sample performance, the results of which indicate that the proposed method is capable of picking up the intricate relationship between response and covariates. Finally, a real data analysis is provided to demonstrate the validity and effectiveness of the proposed method.

Variable selection for nonlinear Cox regression model via deep learning

Variable selection problem for the nonlinear Cox regression model is considered. In survival analysis, one main objective is to identify the covariates that are associated with the risk of experiencing the event of interest. The Cox proportional hazard model is being used extensively in survival analysis in studying the relationship between survival times and covariates, where the model assumes that the covariate has a log-linear effect on the hazard function. However, this linearity assumption may not be satisfied in practice. In order to extract a representative subset of features, various variable selection approaches have been proposed for survival data under the linear Cox model. However, there exists little literature on variable selection for the nonlinear Cox model. To break this gap, we extend the recently developed deep learning-based variable selection model LassoNet to survival data. Simulations are provided to demonstrate the validity and effectiveness of the proposed method. Finally, we apply the proposed methodology to analyze a real data set on diffuse large B-cell lymphoma.

Deep Feature Screening: Feature Selection for Ultra High-Dimensional Data via Deep Neural Networks

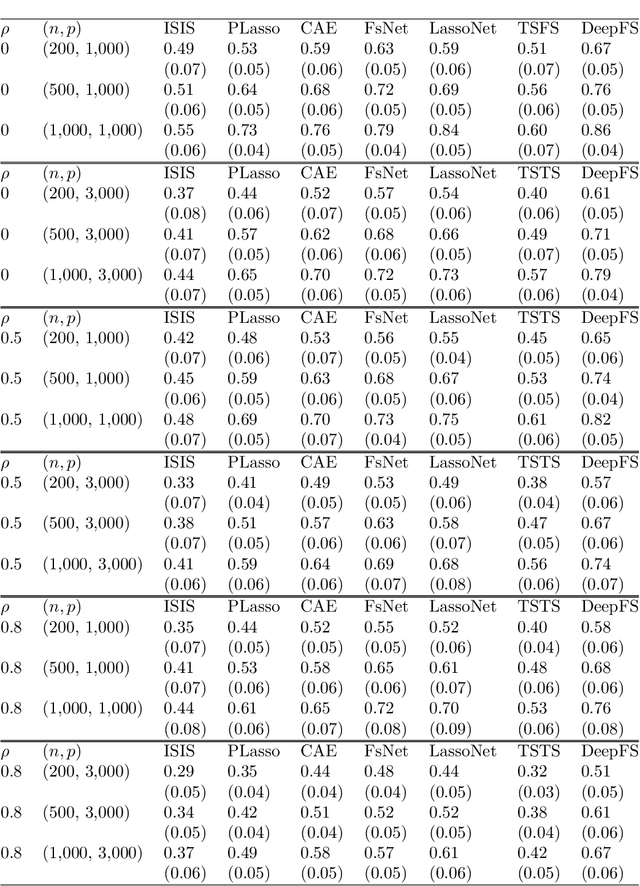
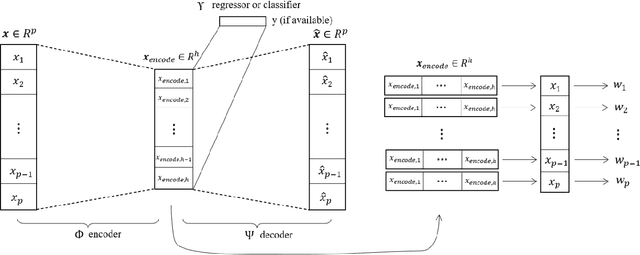
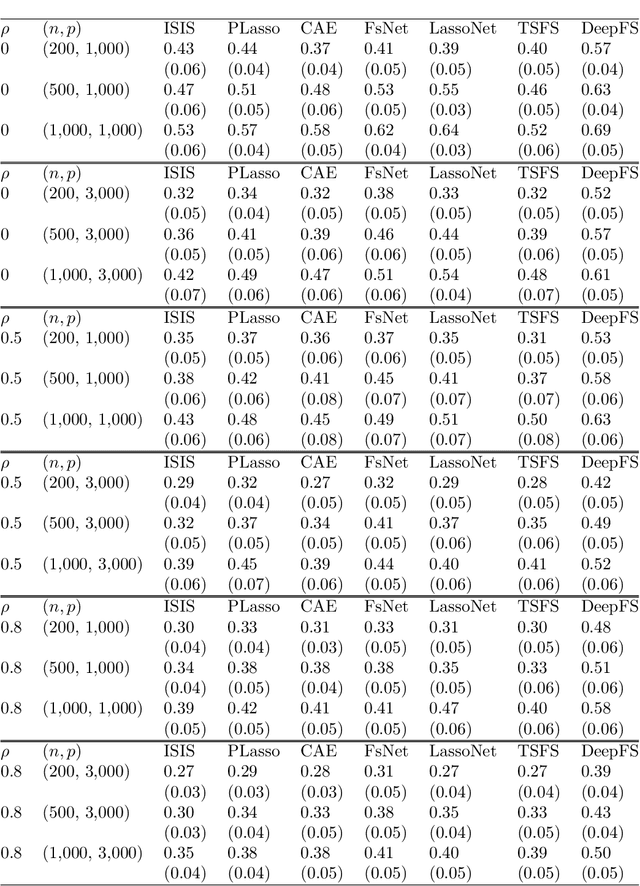
The applications of traditional statistical feature selection methods to high-dimension, low sample-size data often struggle and encounter challenging problems, such as overfitting, curse of dimensionality, computational infeasibility, and strong model assumption. In this paper, we propose a novel two-step nonparametric approach called Deep Feature Screening (DeepFS) that can overcome these problems and identify significant features with high precision for ultra high-dimensional, low-sample-size data. This approach first extracts a low-dimensional representation of input data and then applies feature screening based on multivariate rank distance correlation recently developed by Deb and Sen (2021). This approach combines the strengths of both deep neural networks and feature screening, and thereby has the following appealing features in addition to its ability of handling ultra high-dimensional data with small number of samples: (1) it is model free and distribution free; (2) it can be used for both supervised and unsupervised feature selection; and (3) it is capable of recovering the original input data. The superiority of DeepFS is demonstrated via extensive simulation studies and real data analyses.

Calibrating multi-dimensional complex ODE from noisy data via deep neural networks

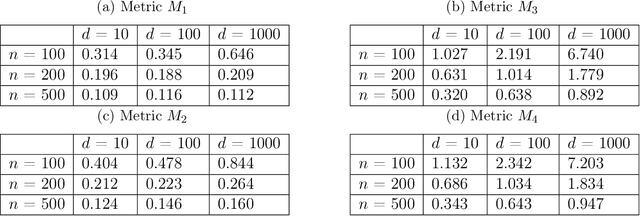
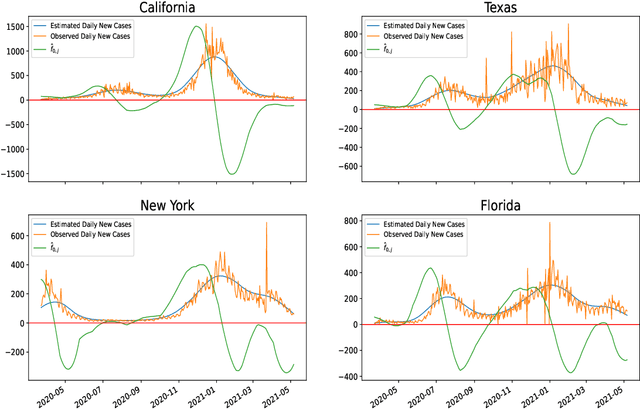
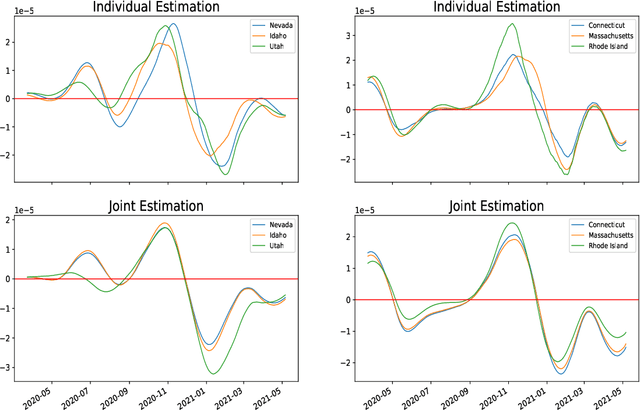
Ordinary differential equations (ODEs) are widely used to model complex dynamics that arises in biology, chemistry, engineering, finance, physics, etc. Calibration of a complicated ODE system using noisy data is generally very difficult. In this work, we propose a two-stage nonparametric approach to address this problem. We first extract the de-noised data and their higher order derivatives using boundary kernel method, and then feed them into a sparsely connected deep neural network with ReLU activation function. Our method is able to recover the ODE system without being subject to the curse of dimensionality and complicated ODE structure. When the ODE possesses a general modular structure, with each modular component involving only a few input variables, and the network architecture is properly chosen, our method is proven to be consistent. Theoretical properties are corroborated by an extensive simulation study that demonstrates the validity and effectiveness of the proposed method. Finally, we use our method to simultaneously characterize the growth rate of Covid-19 infection cases from 50 states of the USA.