Row-clustering of a Point Process-valued Matrix

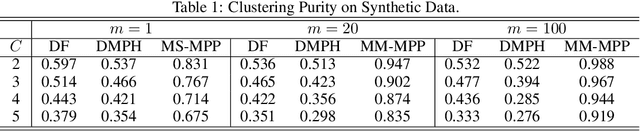
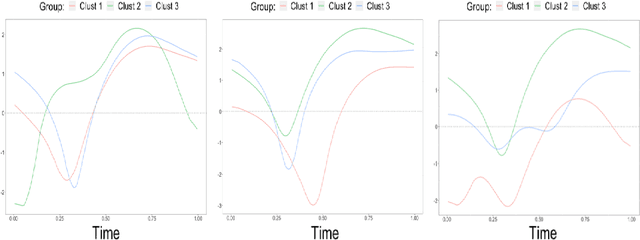
Structured point process data harvested from various platforms poses new challenges to the machine learning community. By imposing a matrix structure to repeatedly observed marked point processes, we propose a novel mixture model of multi-level marked point processes for identifying potential heterogeneity in the observed data. Specifically, we study a matrix whose entries are marked log-Gaussian Cox processes and cluster rows of such a matrix. An efficient semi-parametric Expectation-Solution (ES) algorithm combined with functional principal component analysis (FPCA) of point processes is proposed for model estimation. The effectiveness of the proposed framework is demonstrated through simulation studies and a real data analysis.

Distributed Adaptive Nearest Neighbor Classifier: Algorithm and Theory

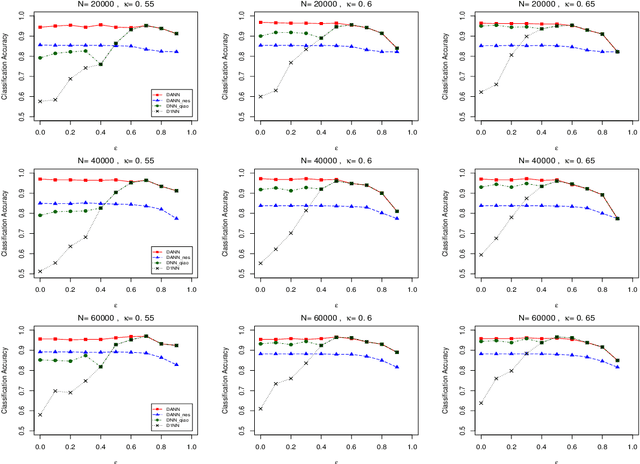
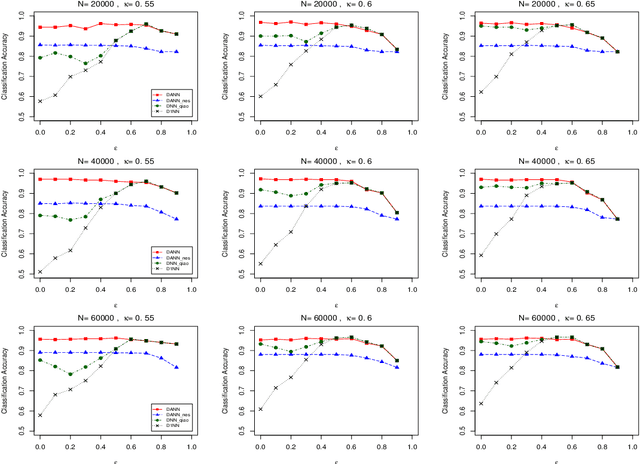
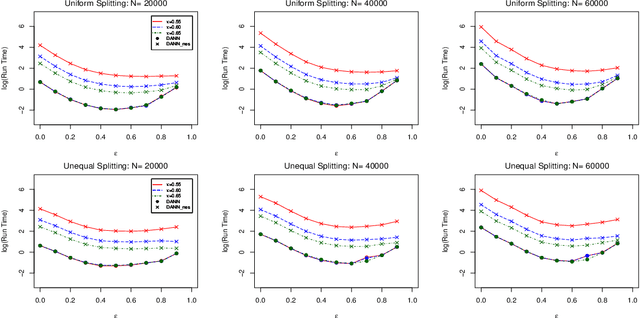
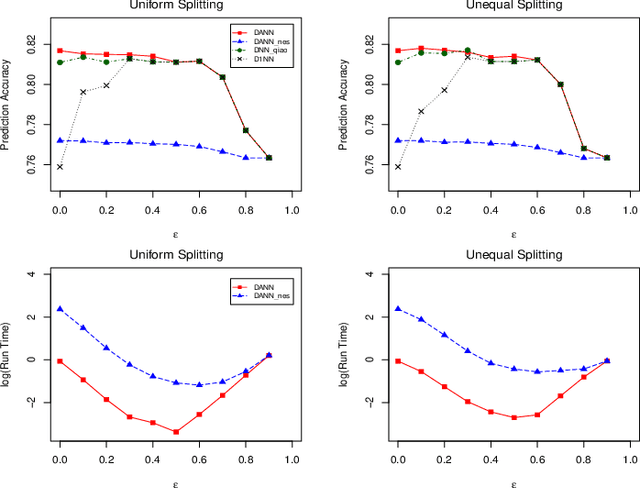
When data is of an extraordinarily large size or physically stored in different locations, the distributed nearest neighbor (NN) classifier is an attractive tool for classification. We propose a novel distributed adaptive NN classifier for which the number of nearest neighbors is a tuning parameter stochastically chosen by a data-driven criterion. An early stopping rule is proposed when searching for the optimal tuning parameter, which not only speeds up the computation but also improves the finite sample performance of the proposed Algorithm. Convergence rate of excess risk of the distributed adaptive NN classifier is investigated under various sub-sample size compositions. In particular, we show that when the sub-sample sizes are sufficiently large, the proposed classifier achieves the nearly optimal convergence rate. Effectiveness of the proposed approach is demonstrated through simulation studies as well as an empirical application to a real-world dataset.

Optimal Nonparametric Inference under Quantization

Statistical inference based on lossy or incomplete samples is of fundamental importance in research areas such as signal/image processing, medical image storage, remote sensing, signal transmission. In this paper, we propose a nonparametric testing procedure based on quantized samples. In contrast to the classic nonparametric approach, our method lives on a coarse grid of sample information and are simple-to-use. Under mild technical conditions, we establish the asymptotic properties of the proposed procedures including asymptotic null distribution of the quantization test statistic as well as its minimax power optimality. Concrete quantizers are constructed for achieving the minimax optimality in practical use. Simulation results and a real data analysis are provided to demonstrate the validity and effectiveness of the proposed test. Our work bridges the classical nonparametric inference to modern lossy data setting.

Optimal tuning for divide-and-conquer kernel ridge regression with massive data

We propose a first data-driven tuning procedure for divide-and-conquer kernel ridge regression (Zhang et al., 2015). While the proposed criterion is computationally scalable for massive data sets, it is also shown to be asymptotically optimal under mild conditions. The effectiveness of our method is illustrated by extensive simulations and an application to Million Song Dataset.