Deep Neural Network Classifier for Multi-dimensional Functional Data

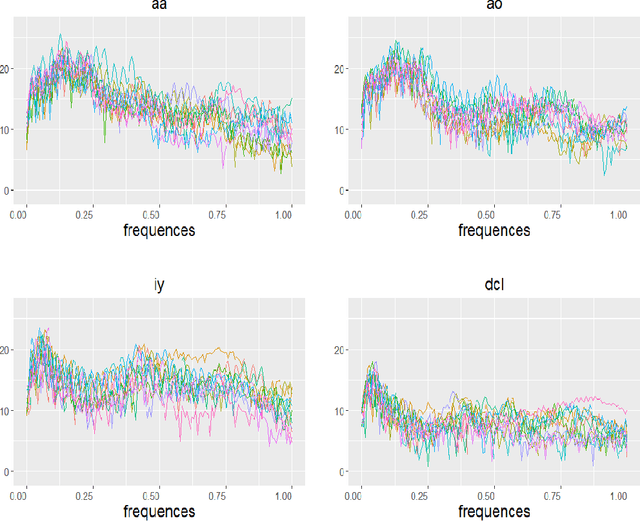
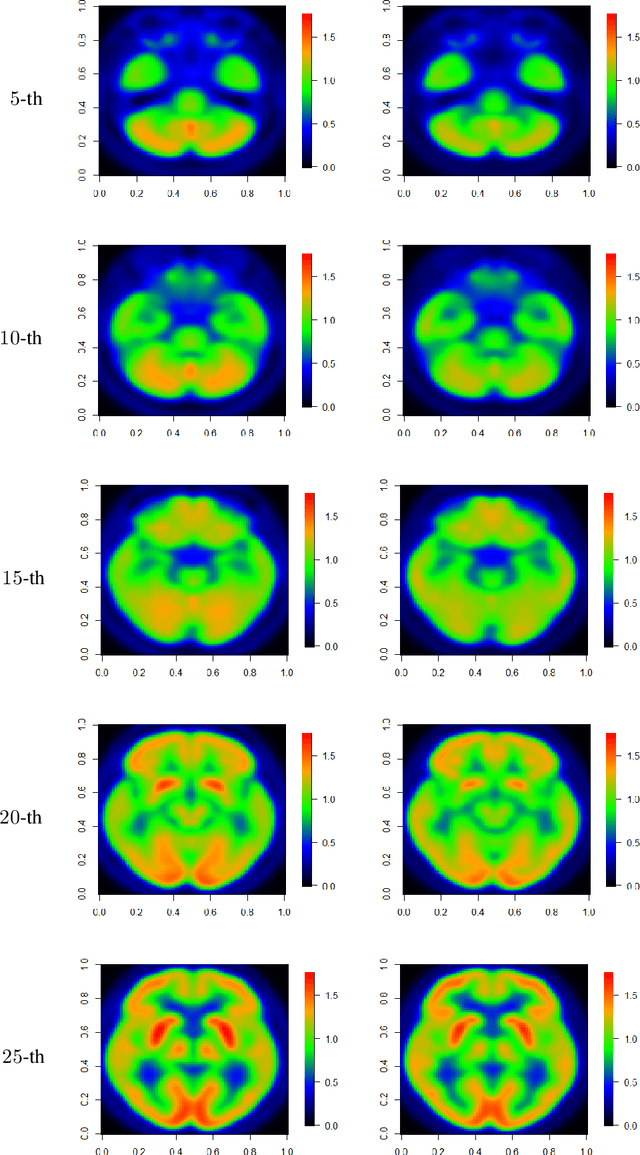
We propose a new approach, called as functional deep neural network (FDNN), for classifying multi-dimensional functional data. Specifically, a deep neural network is trained based on the principle components of the training data which shall be used to predict the class label of a future data function. Unlike the popular functional discriminant analysis approaches which rely on Gaussian assumption, the proposed FDNN approach applies to general non-Gaussian multi-dimensional functional data. Moreover, when the log density ratio possesses a locally connected functional modular structure, we show that FDNN achieves minimax optimality. The superiority of our approach is demonstrated through both simulated and real-world datasets.