YOLO-FireAD: Efficient Fire Detection via Attention-Guided Inverted Residual Learning and Dual-Pooling Feature Preservation

Fire detection in dynamic environments faces continuous challenges, including the interference of illumination changes, many false detections or missed detections, and it is difficult to achieve both efficiency and accuracy. To address the problem of feature extraction limitation and information loss in the existing YOLO-based models, this study propose You Only Look Once for Fire Detection with Attention-guided Inverted Residual and Dual-pooling Downscale Fusion (YOLO-FireAD) with two core innovations: (1) Attention-guided Inverted Residual Block (AIR) integrates hybrid channel-spatial attention with inverted residuals to adaptively enhance fire features and suppress environmental noise; (2) Dual Pool Downscale Fusion Block (DPDF) preserves multi-scale fire patterns through learnable fusion of max-average pooling outputs, mitigating small-fire detection failures. Extensive evaluation on two public datasets shows the efficient performance of our model. Our proposed model keeps the sum amount of parameters (1.45M, 51.8% lower than YOLOv8n) (4.6G, 43.2% lower than YOLOv8n), and mAP75 is higher than the mainstream real-time object detection models YOLOv8n, YOL-Ov9t, YOLOv10n, YOLO11n, YOLOv12n and other YOLOv8 variants 1.3-5.5%.

Multiclass classification for multidimensional functional data through deep neural networks

The intrinsically infinite-dimensional features of the functional observations over multidimensional domains render the standard classification methods effectively inapplicable. To address this problem, we introduce a novel multiclass functional deep neural network (mfDNN) classifier as an innovative data mining and classification tool. Specifically, we consider sparse deep neural network architecture with rectifier linear unit (ReLU) activation function and minimize the cross-entropy loss in the multiclass classification setup. This neural network architecture allows us to employ modern computational tools in the implementation. The convergence rates of the misclassification risk functions are also derived for both fully observed and discretely observed multidimensional functional data. We demonstrate the performance of mfDNN on simulated data and several benchmark datasets from different application domains.

Robust Deep Neural Network Estimation for Multi-dimensional Functional Data

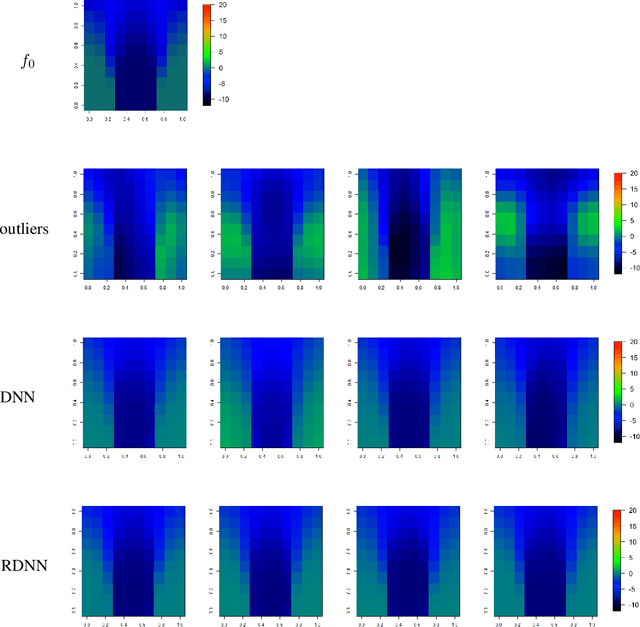
In this paper, we propose a robust estimator for the location function from multi-dimensional functional data. The proposed estimators are based on the deep neural networks with ReLU activation function. At the meanwhile, the estimators are less susceptible to outlying observations and model-misspecification. For any multi-dimensional functional data, we provide the uniform convergence rates for the proposed robust deep neural networks estimators. Simulation studies illustrate the competitive performance of the robust deep neural network estimators on regular data and their superior performance on data that contain anomalies. The proposed method is also applied to analyze 2D and 3D images of patients with Alzheimer's disease obtained from the Alzheimer Disease Neuroimaging Initiative database.

Deep Neural Network Classifier for Multi-dimensional Functional Data

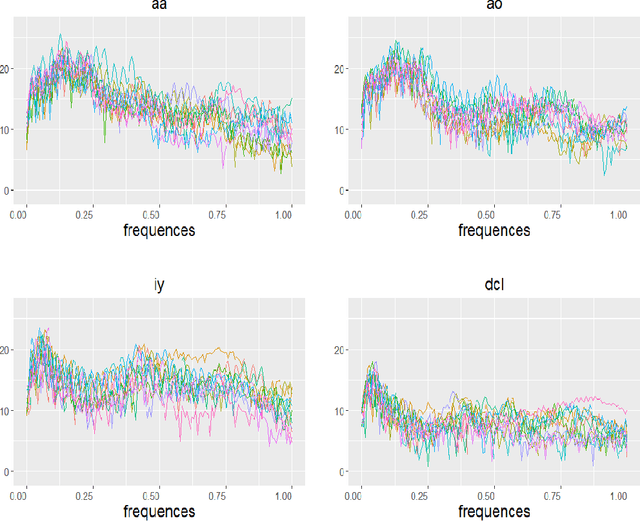
We propose a new approach, called as functional deep neural network (FDNN), for classifying multi-dimensional functional data. Specifically, a deep neural network is trained based on the principle components of the training data which shall be used to predict the class label of a future data function. Unlike the popular functional discriminant analysis approaches which rely on Gaussian assumption, the proposed FDNN approach applies to general non-Gaussian multi-dimensional functional data. Moreover, when the log density ratio possesses a locally connected functional modular structure, we show that FDNN achieves minimax optimality. The superiority of our approach is demonstrated through both simulated and real-world datasets.

Estimation of the Mean Function of Functional Data via Deep Neural Networks

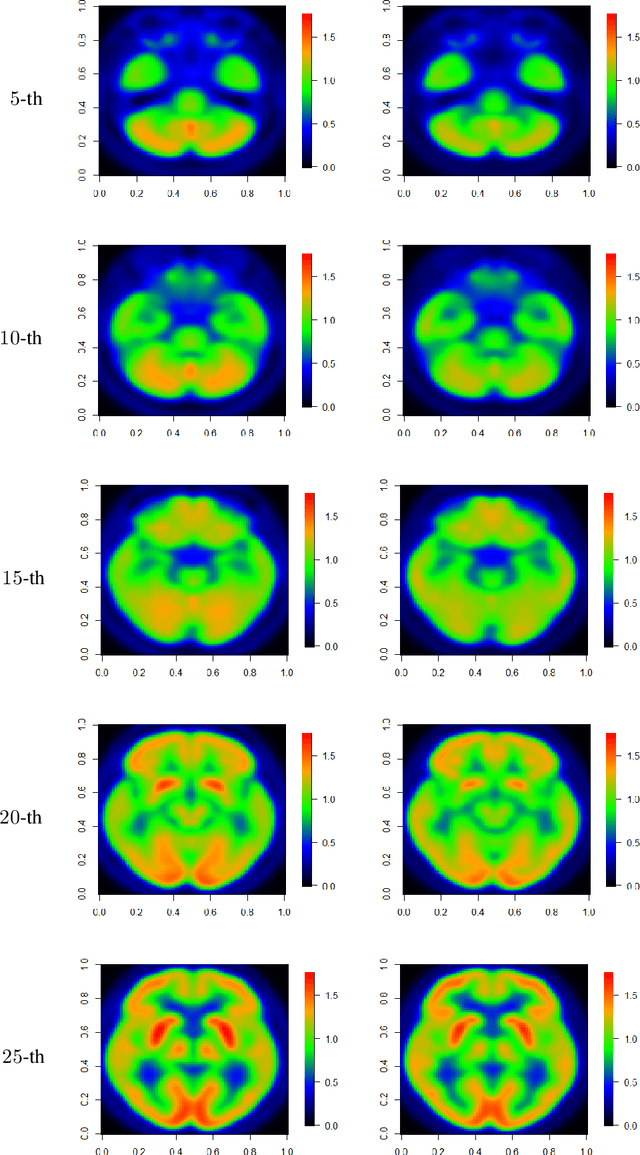
In this work, we propose a deep neural network method to perform nonparametric regression for functional data. The proposed estimators are based on sparsely connected deep neural networks with ReLU activation function. By properly choosing network architecture, our estimator achieves the optimal nonparametric convergence rate in empirical norm. Under certain circumstances such as trigonometric polynomial kernel and a sufficiently large sampling frequency, the convergence rate is even faster than root-$n$ rate. Through Monte Carlo simulation studies we examine the finite-sample performance of the proposed method. Finally, the proposed method is applied to analyze positron emission tomography images of patients with Alzheimer disease obtained from the Alzheimer Disease Neuroimaging Initiative database.