Amplitude Mean of Functional Data on $\mathbb{S}^2$

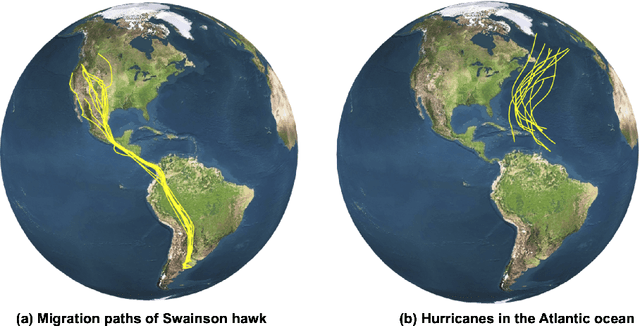
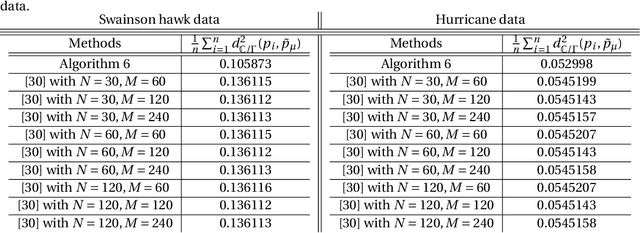
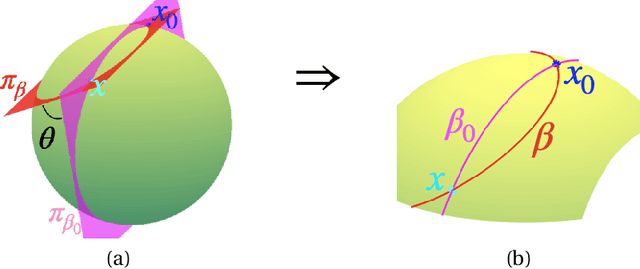
Manifold-valued functional data analysis (FDA) recently becomes an active area of research motivated by the raising availability of trajectories or longitudinal data observed on non-linear manifolds. The challenges of analyzing such data come from many aspects, including infinite dimensionality and nonlinearity, as well as time-domain or phase variability. In this paper, we study the amplitude part of manifold-valued functions on $\mathbb{S}^2$, which is invariant to random time warping or re-parameterization. Utilizing the nice geometry of $\mathbb{S}^2$, we develop a set of efficient and accurate tools for temporal alignment of functions, geodesic computing, and sample mean calculation. At the heart of these tools, they rely on gradient descent algorithms with carefully derived gradients. We show the advantages of these newly developed tools over its competitors with extensive simulations and real data and demonstrate the importance of considering the amplitude part of functions instead of mixing it with phase variability in manifold-valued FDA.

Accelerated Algorithms for Convex and Non-Convex Optimization on Manifolds

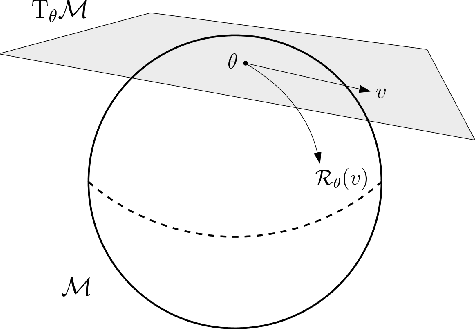
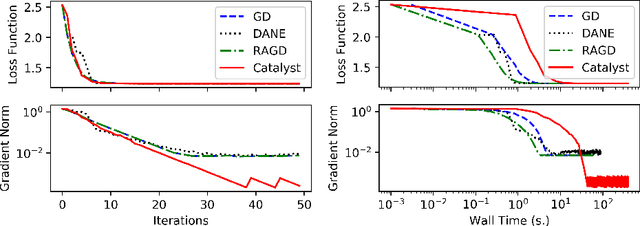
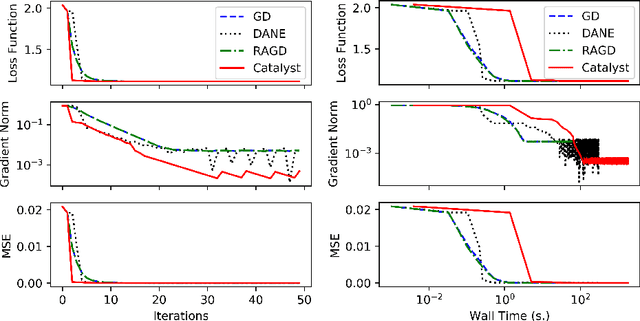
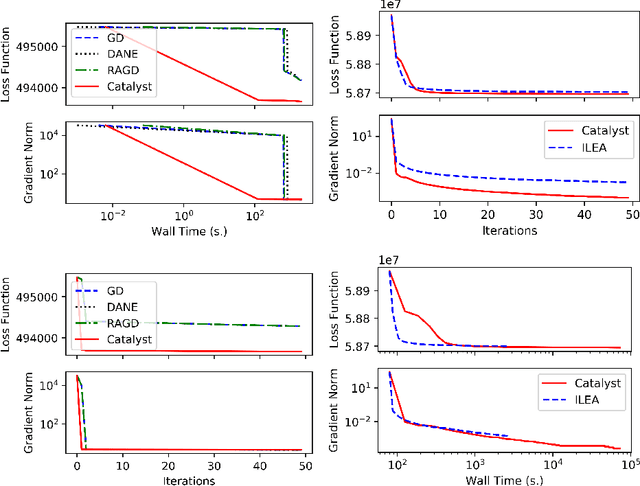
We propose a general scheme for solving convex and non-convex optimization problems on manifolds. The central idea is that, by adding a multiple of the squared retraction distance to the objective function in question, we "convexify" the objective function and solve a series of convex sub-problems in the optimization procedure. One of the key challenges for optimization on manifolds is the difficulty of verifying the complexity of the objective function, e.g., whether the objective function is convex or non-convex, and the degree of non-convexity. Our proposed algorithm adapts to the level of complexity in the objective function. We show that when the objective function is convex, the algorithm provably converges to the optimum and leads to accelerated convergence. When the objective function is non-convex, the algorithm will converge to a stationary point. Our proposed method unifies insights from Nesterov's original idea for accelerating gradient descent algorithms with recent developments in optimization algorithms in Euclidean space. We demonstrate the utility of our algorithms on several manifold optimization tasks such as estimating intrinsic and extrinsic Fr\'echet means on spheres and low-rank matrix factorization with Grassmann manifolds applied to the Netflix rating data set.

Communication Efficient Parallel Algorithms for Optimization on Manifolds

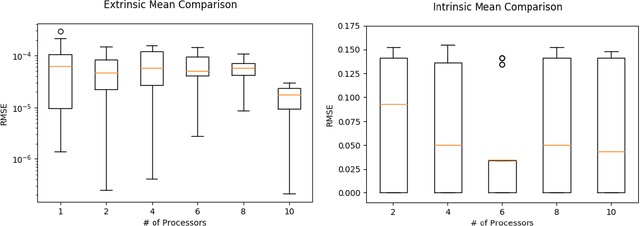
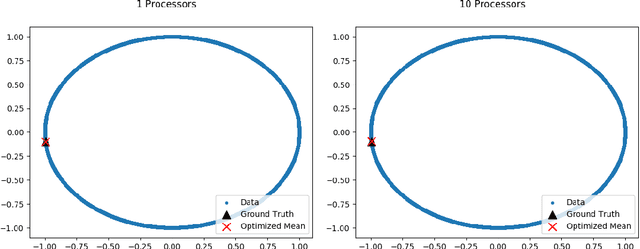
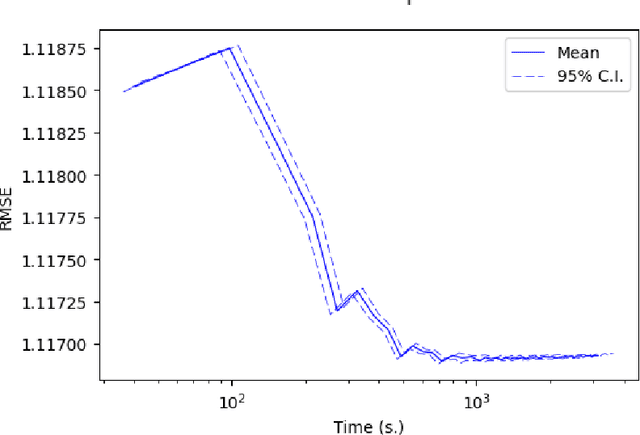
The last decade has witnessed an explosion in the development of models, theory and computational algorithms for "big data" analysis. In particular, distributed computing has served as a natural and dominating paradigm for statistical inference. However, the existing literature on parallel inference almost exclusively focuses on Euclidean data and parameters. While this assumption is valid for many applications, it is increasingly more common to encounter problems where the data or the parameters lie on a non-Euclidean space, like a manifold for example. Our work aims to fill a critical gap in the literature by generalizing parallel inference algorithms to optimization on manifolds. We show that our proposed algorithm is both communication efficient and carries theoretical convergence guarantees. In addition, we demonstrate the performance of our algorithm to the estimation of Fr\'echet means on simulated spherical data and the low-rank matrix completion problem over Grassmann manifolds applied to the Netflix prize data set.