Accelerated Algorithms for Convex and Non-Convex Optimization on Manifolds
Paper and Code
Oct 18, 2020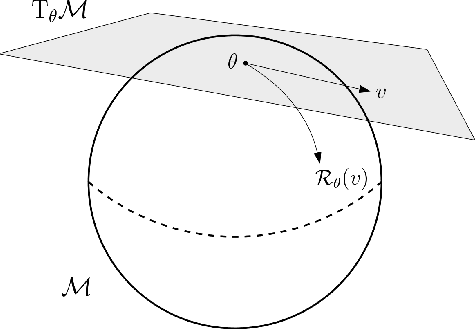
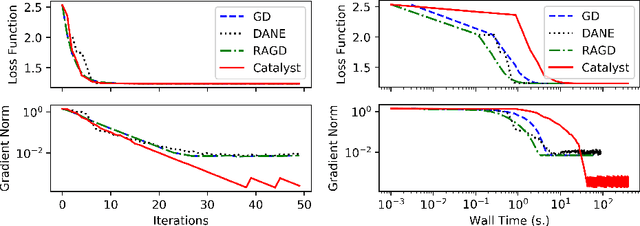
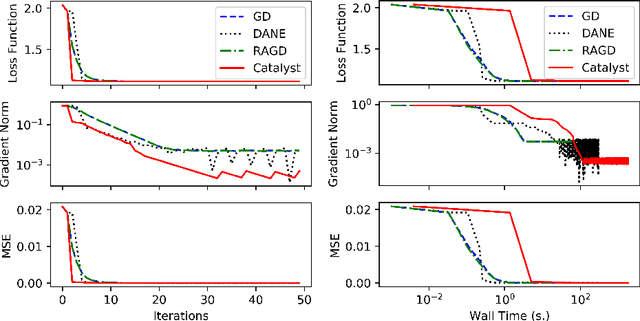
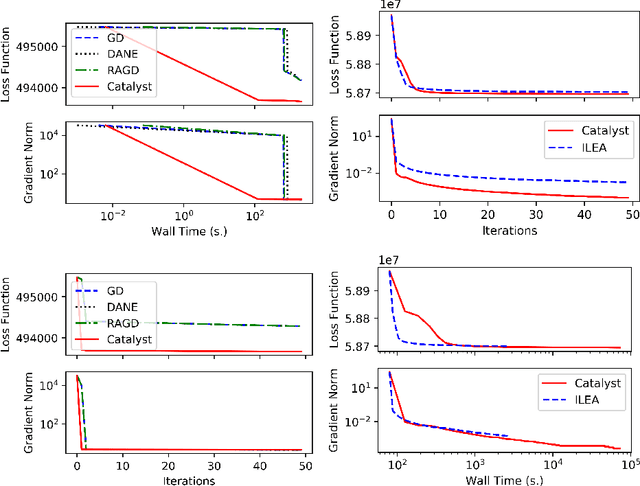
We propose a general scheme for solving convex and non-convex optimization problems on manifolds. The central idea is that, by adding a multiple of the squared retraction distance to the objective function in question, we "convexify" the objective function and solve a series of convex sub-problems in the optimization procedure. One of the key challenges for optimization on manifolds is the difficulty of verifying the complexity of the objective function, e.g., whether the objective function is convex or non-convex, and the degree of non-convexity. Our proposed algorithm adapts to the level of complexity in the objective function. We show that when the objective function is convex, the algorithm provably converges to the optimum and leads to accelerated convergence. When the objective function is non-convex, the algorithm will converge to a stationary point. Our proposed method unifies insights from Nesterov's original idea for accelerating gradient descent algorithms with recent developments in optimization algorithms in Euclidean space. We demonstrate the utility of our algorithms on several manifold optimization tasks such as estimating intrinsic and extrinsic Fr\'echet means on spheres and low-rank matrix factorization with Grassmann manifolds applied to the Netflix rating data set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge