Partial Non-rigid Deformations and interpolations of Human Body Surfaces

Non-rigid shape deformations pose significant challenges, and most existing methods struggle to handle partial deformations effectively. We present Partial Non-rigid Deformations and interpolations of the human body Surfaces (PaNDAS), a new method to learn local and global deformations of 3D surface meshes by building on recent deep models. Unlike previous approaches, our method enables restricting deformations to specific parts of the shape in a versatile way and allows for mixing and combining various poses from the database, all while not requiring any optimization at inference time. We demonstrate that the proposed framework can be used to generate new shapes, interpolate between parts of shapes, and perform other shape manipulation tasks with state-of-the-art accuracy and greater locality across various types of human surface data. Code and data will be made available soon.

Basis restricted elastic shape analysis on the space of unregistered surfaces

This paper introduces a new mathematical and numerical framework for surface analysis derived from the general setting of elastic Riemannian metrics on shape spaces. Traditionally, those metrics are defined over the infinite dimensional manifold of immersed surfaces and satisfy specific invariance properties enabling the comparison of surfaces modulo shape preserving transformations such as reparametrizations. The specificity of the approach we develop is to restrict the space of allowable transformations to predefined finite dimensional bases of deformation fields. These are estimated in a data-driven way so as to emulate specific types of surface transformations observed in a training set. The use of such bases allows to simplify the representation of the corresponding shape space to a finite dimensional latent space. However, in sharp contrast with methods involving e.g. mesh autoencoders, the latent space is here equipped with a non-Euclidean Riemannian metric precisely inherited from the family of aforementioned elastic metrics. We demonstrate how this basis restricted model can be then effectively implemented to perform a variety of tasks on surface meshes which, importantly, does not assume these to be pre-registered (i.e. with given point correspondences) or to even have a consistent mesh structure. We specifically validate our approach on human body shape and pose data as well as human face scans, and show how it generally outperforms state-of-the-art methods on problems such as shape registration, interpolation, motion transfer or random pose generation.

VariGrad: A Novel Feature Vector Architecture for Geometric Deep Learning on Unregistered Data

We present a novel geometric deep learning layer that leverages the varifold gradient (VariGrad) to compute feature vector representations of 3D geometric data. These feature vectors can be used in a variety of downstream learning tasks such as classification, registration, and shape reconstruction. Our model's use of parameterization independent varifold representations of geometric data allows our model to be both trained and tested on data independent of the given sampling or parameterization. We demonstrate the efficiency, generalizability, and robustness to resampling demonstrated by the proposed VariGrad layer.

Toward Mesh-Invariant 3D Generative Deep Learning with Geometric Measures

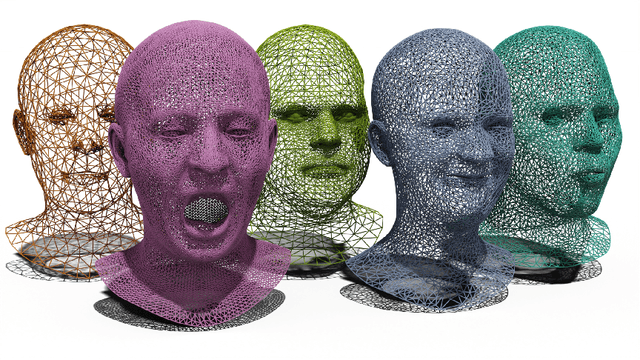
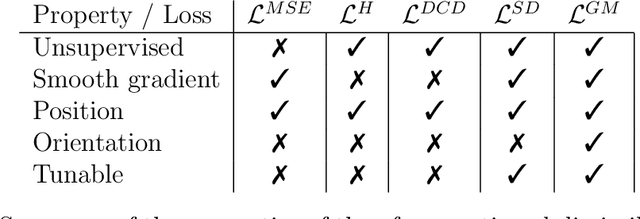
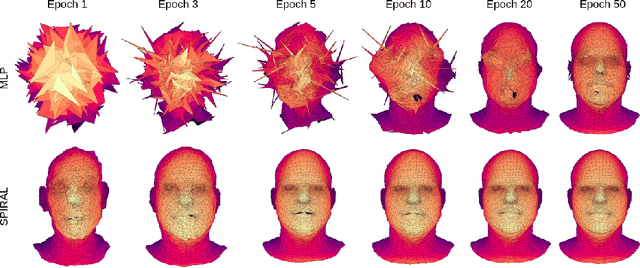
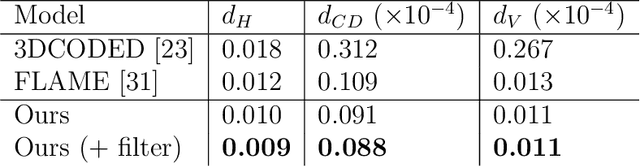
3D generative modeling is accelerating as the technology allowing the capture of geometric data is developing. However, the acquired data is often inconsistent, resulting in unregistered meshes or point clouds. Many generative learning algorithms require correspondence between each point when comparing the predicted shape and the target shape. We propose an architecture able to cope with different parameterizations, even during the training phase. In particular, our loss function is built upon a kernel-based metric over a representation of meshes using geometric measures such as currents and varifolds. The latter allows to implement an efficient dissimilarity measure with many desirable properties such as robustness to resampling of the mesh or point cloud. We demonstrate the efficiency and resilience of our model with a generative learning task of human faces.

BaRe-ESA: A Riemannian Framework for Unregistered Human Body Shapes

We present BaRe-ESA, a novel Riemannian framework for human body scan representation, interpolation and extrapolation. BaRe-ESA operates directly on unregistered meshes, i.e., without the need to establish prior point to point correspondences or to assume a consistent mesh structure. Our method relies on a latent space representation, which is equipped with a Riemannian (non-Euclidean) metric associated to an invariant higher-order metric on the space of surfaces. Experimental results on the FAUST and DFAUST datasets show that BaRe-ESA brings significant improvements with respect to previous solutions in terms of shape registration, interpolation and extrapolation. The efficiency and strength of our model is further demonstrated in applications such as motion transfer and random generation of body shape and pose.

3D Shape Sequence of Human Comparison and Classification using Current and Varifolds

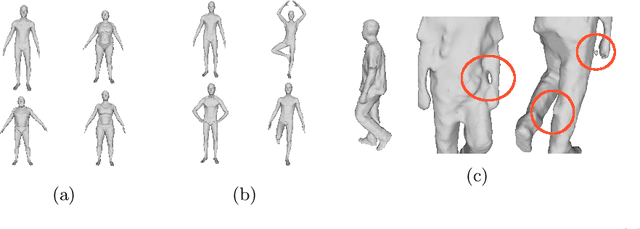
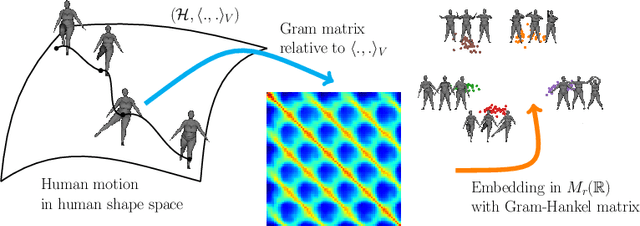
In this paper we address the task of the comparison and the classification of 3D shape sequences of human. The non-linear dynamics of the human motion and the changing of the surface parametrization over the time make this task very challenging. To tackle this issue, we propose to embed the 3D shape sequences in an infinite dimensional space, the space of varifolds, endowed with an inner product that comes from a given positive definite kernel. More specifically, our approach involves two steps: 1) the surfaces are represented as varifolds, this representation induces metrics equivariant to rigid motions and invariant to parametrization; 2) the sequences of 3D shapes are represented by Gram matrices derived from their infinite dimensional Hankel matrices. The problem of comparison of two 3D sequences of human is formulated as a comparison of two Gram-Hankel matrices. Extensive experiments on CVSSP3D and Dyna datasets show that our method is competitive with state-of-the-art in 3D human sequence motion retrieval. Code for the experiments is available at https://github.com/CRISTAL-3DSAM/HumanComparisonVarifolds.

A Riemannian Framework for Analysis of Human Body Surface

We propose a novel framework for comparing 3D human shapes under the change of shape and pose. This problem is challenging since 3D human shapes vary significantly across subjects and body postures. We solve this problem by using a Riemannian approach. Our core contribution is the mapping of the human body surface to the space of metrics and normals. We equip this space with a family of Riemannian metrics, called Ebin (or DeWitt) metrics. We treat a human body surface as a point in a "shape space" equipped with a family of Riemmanian metrics. The family of metrics is invariant under rigid motions and reparametrizations; hence it induces a metric on the "shape space" of surfaces. Using the alignment of human bodies with a given template, we show that this family of metrics allows us to distinguish the changes in shape and pose. The proposed framework has several advantages. First, we define family of metrics with desired invariant properties for the comparison of human shape. Second, we present an efficient framework to compute geodesic paths between human shape given the chosen metric. Third, this framework provides some basic tools for statistical shape analysis of human body surfaces. Finally, we demonstrate the utility of the proposed framework in pose and shape retrieval of human body.