Measuring Feature Dependency of Neural Networks by Collapsing Feature Dimensions in the Data Manifold

This paper introduces a new technique to measure the feature dependency of neural network models. The motivation is to better understand a model by querying whether it is using information from human-understandable features, e.g., anatomical shape, volume, or image texture. Our method is based on the principle that if a model is dependent on a feature, then removal of that feature should significantly harm its performance. A targeted feature is "removed" by collapsing the dimension in the data distribution that corresponds to that feature. We perform this by moving data points along the feature dimension to a baseline feature value while staying on the data manifold, as estimated by a deep generative model. Then we observe how the model's performance changes on the modified test data set, with the target feature dimension removed. We test our method on deep neural network models trained on synthetic image data with known ground truth, an Alzheimer's disease prediction task using MRI and hippocampus segmentations from the OASIS-3 dataset, and a cell nuclei classification task using the Lizard dataset.

Learning Spatially-Continuous Fiber Orientation Functions

Our understanding of the human connectome is fundamentally limited by the resolution of diffusion MR images. Reconstructing a connectome's constituent neural pathways with tractography requires following a continuous field of fiber directions. Typically, this field is found with simple trilinear interpolation in low-resolution, noisy diffusion MRIs. However, trilinear interpolation struggles following fine-scale changes in low-quality data. Recent deep learning methods in super-resolving diffusion MRIs have focused on upsampling to a fixed spatial grid, but this does not satisfy tractography's need for a continuous field. In this work, we propose FENRI, a novel method that learns spatially-continuous fiber orientation density functions from low-resolution diffusion-weighted images. To quantify FENRI's capabilities in tractography, we also introduce an expanded simulated dataset built for evaluating deep-learning tractography models. We demonstrate that FENRI accurately predicts high-resolution fiber orientations from realistic low-quality data, and that FENRI-based tractography offers improved streamline reconstruction over the current use of trilinear interpolation.

Quantifying Hippocampal Shape Asymmetry in Alzheimer's Disease Using Optimal Shape Correspondences

Hippocampal atrophy in Alzheimer's disease (AD) is asymmetric and spatially inhomogeneous. While extensive work has been done on volume and shape analysis of atrophy of the hippocampus in AD, less attention has been given to hippocampal asymmetry specifically. Previous studies of hippocampal asymmetry are limited to global volume or shape measures, which don't localize shape asymmetry at the point level. In this paper, we propose to quantify localized shape asymmetry by optimizing point correspondences between left and right hippocampi within a subject, while simultaneously favoring a compact statistical shape model of the entire sample. To account for related variables that have impact on AD and healthy subject differences, we build linear models with other confounding factors. Our results on the OASIS3 dataset demonstrate that compared to using volumetric information, shape asymmetry reveals fine-grained, localized differences that indicate the hippocampal regions of most significant shape asymmetry in AD patients.

Feature Gradient Flow for Interpreting Deep Neural Networks in Head and Neck Cancer Prediction

This paper introduces feature gradient flow, a new technique for interpreting deep learning models in terms of features that are understandable to humans. The gradient flow of a model locally defines nonlinear coordinates in the input data space representing the information the model is using to make its decisions. Our idea is to measure the agreement of interpretable features with the gradient flow of a model. To then evaluate the importance of a particular feature to the model, we compare that feature's gradient flow measure versus that of a baseline noise feature. We then develop a technique for training neural networks to be more interpretable by adding a regularization term to the loss function that encourages the model gradients to align with those of chosen interpretable features. We test our method in a convolutional neural network prediction of distant metastasis of head and neck cancer from a computed tomography dataset from the Cancer Imaging Archive.

NASDM: Nuclei-Aware Semantic Histopathology Image Generation Using Diffusion Models

In recent years, computational pathology has seen tremendous progress driven by deep learning methods in segmentation and classification tasks aiding prognostic and diagnostic settings. Nuclei segmentation, for instance, is an important task for diagnosing different cancers. However, training deep learning models for nuclei segmentation requires large amounts of annotated data, which is expensive to collect and label. This necessitates explorations into generative modeling of histopathological images. In this work, we use recent advances in conditional diffusion modeling to formulate a first-of-its-kind nuclei-aware semantic tissue generation framework (NASDM) which can synthesize realistic tissue samples given a semantic instance mask of up to six different nuclei types, enabling pixel-perfect nuclei localization in generated samples. These synthetic images are useful in applications in pathology pedagogy, validation of models, and supplementation of existing nuclei segmentation datasets. We demonstrate that NASDM is able to synthesize high-quality histopathology images of the colon with superior quality and semantic controllability over existing generative methods.

Deep Learning the Shape of the Brain Connectome

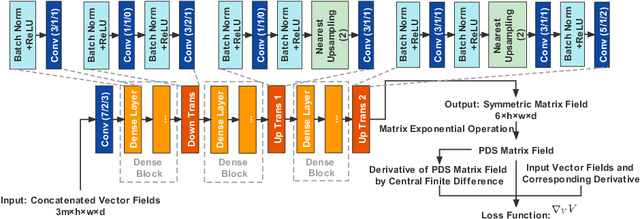
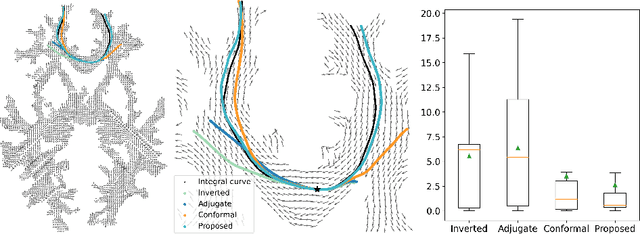
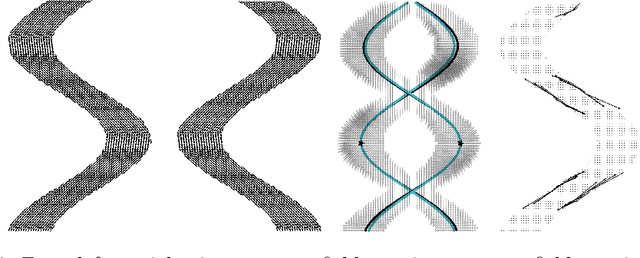
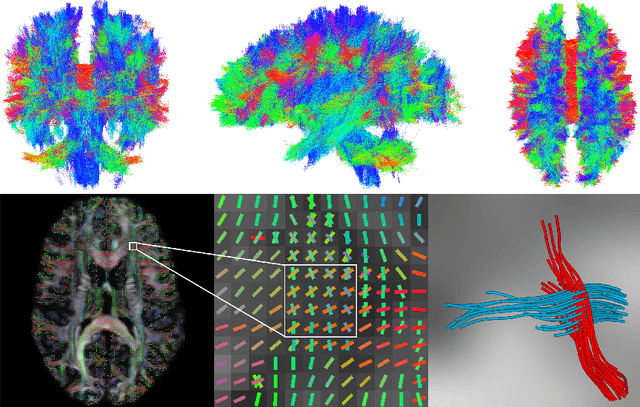
To statistically study the variability and differences between normal and abnormal brain connectomes, a mathematical model of the neural connections is required. In this paper, we represent the brain connectome as a Riemannian manifold, which allows us to model neural connections as geodesics. We show for the first time how one can leverage deep neural networks to estimate a Riemannian metric of the brain that can accommodate fiber crossings and is a natural modeling tool to infer the shape of the brain from DWMRI. Our method achieves excellent performance in geodesic-white-matter-pathway alignment and tackles the long-standing issue in previous methods: the inability to recover the crossing fibers with high fidelity.

Integrated Construction of Multimodal Atlases with Structural Connectomes in the Space of Riemannian Metrics

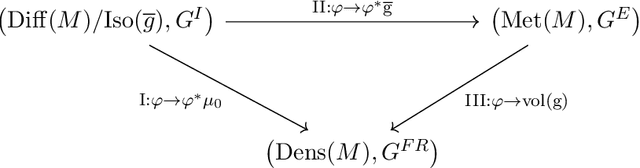
The structural network of the brain, or structural connectome, can be represented by fiber bundles generated by a variety of tractography methods. While such methods give qualitative insights into brain structure, there is controversy over whether they can provide quantitative information, especially at the population level. In order to enable population-level statistical analysis of the structural connectome, we propose representing a connectome as a Riemannian metric, which is a point on an infinite-dimensional manifold. We equip this manifold with the Ebin metric, a natural metric structure for this space, to get a Riemannian manifold along with its associated geometric properties. We then use this Riemannian framework to apply object-oriented statistical analysis to define an atlas as the Fr\'echet mean of a population of Riemannian metrics. This formulation ties into the existing framework for diffeomorphic construction of image atlases, allowing us to construct a multimodal atlas by simultaneously integrating complementary white matter structure details from DWMRI and cortical details from T1-weighted MRI. We illustrate our framework with 2D data examples of connectome registration and atlas formation. Finally, we build an example 3D multimodal atlas using T1 images and connectomes derived from diffusion tensors estimated from a subset of subjects from the Human Connectome Project.

Structural Connectome Atlas Construction in the Space of Riemannian Metrics

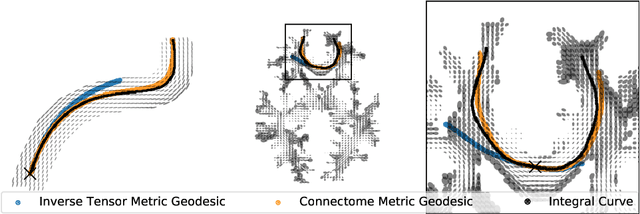
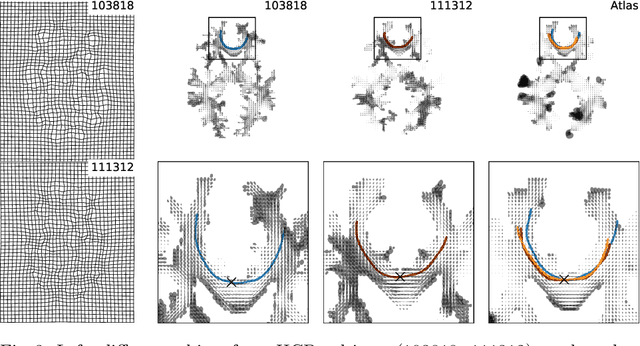
The structural connectome is often represented by fiber bundles generated from various types of tractography. We propose a method of analyzing connectomes by representing them as a Riemannian metric, thereby viewing them as points in an infinite-dimensional manifold. After equipping this space with a natural metric structure, the Ebin metric, we apply object-oriented statistical analysis to define an atlas as the Fr\'echet mean of a population of Riemannian metrics. We demonstrate connectome registration and atlas formation using connectomes derived from diffusion tensors estimated from a subset of subjects from the Human Connectome Project.

The Adversarial Attack and Detection under the Fisher Information Metric

Many deep learning models are vulnerable to the adversarial attack, i.e., imperceptible but intentionally-designed perturbations to the input can cause incorrect output of the networks. In this paper, using information geometry, we provide a reasonable explanation for the vulnerability of deep learning models. By considering the data space as a non-linear space with the Fisher information metric induced from a neural network, we first propose an adversarial attack algorithm termed one-step spectral attack (OSSA). The method is described by a constrained quadratic form of the Fisher information matrix, where the optimal adversarial perturbation is given by the first eigenvector, and the model vulnerability is reflected by the eigenvalues. The larger an eigenvalue is, the more vulnerable the model is to be attacked by the corresponding eigenvector. Taking advantage of the property, we also propose an adversarial detection method with the eigenvalues serving as characteristics. Both our attack and detection algorithms are numerically optimized to work efficiently on large datasets. Our evaluations show superior performance compared with other methods, implying that the Fisher information is a promising approach to investigate the adversarial attacks and defenses.

Semi-supervised Learning with GANs: Manifold Invariance with Improved Inference

Semi-supervised learning methods using Generative Adversarial Networks (GANs) have shown promising empirical success recently. Most of these methods use a shared discriminator/classifier which discriminates real examples from fake while also predicting the class label. Motivated by the ability of the GANs generator to capture the data manifold well, we propose to estimate the tangent space to the data manifold using GANs and employ it to inject invariances into the classifier. In the process, we propose enhancements over existing methods for learning the inverse mapping (i.e., the encoder) which greatly improves in terms of semantic similarity of the reconstructed sample with the input sample. We observe considerable empirical gains in semi-supervised learning over baselines, particularly in the cases when the number of labeled examples is low. We also provide insights into how fake examples influence the semi-supervised learning procedure.