Deep Learning the Shape of the Brain Connectome

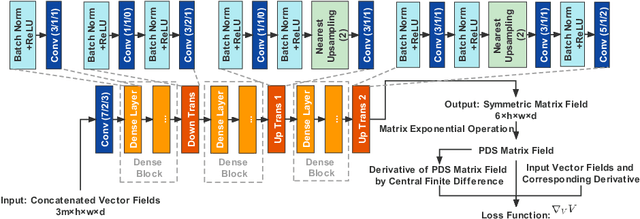
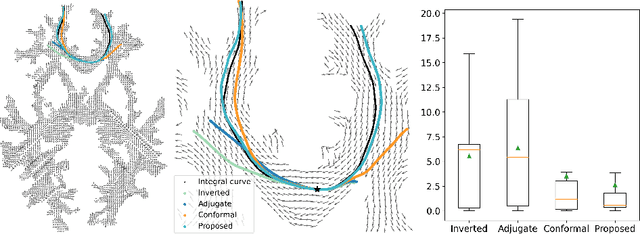
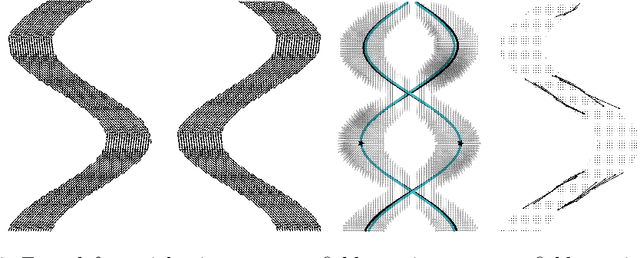
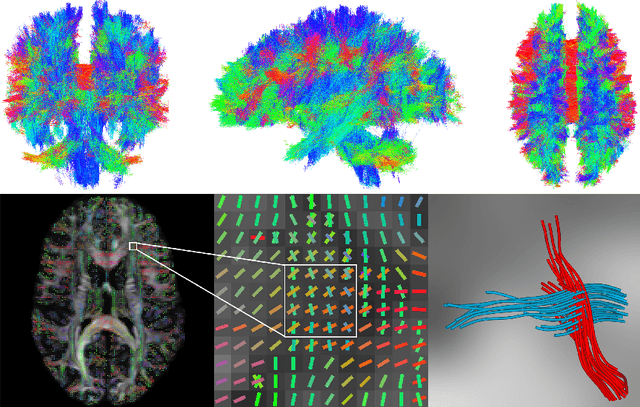
To statistically study the variability and differences between normal and abnormal brain connectomes, a mathematical model of the neural connections is required. In this paper, we represent the brain connectome as a Riemannian manifold, which allows us to model neural connections as geodesics. We show for the first time how one can leverage deep neural networks to estimate a Riemannian metric of the brain that can accommodate fiber crossings and is a natural modeling tool to infer the shape of the brain from DWMRI. Our method achieves excellent performance in geodesic-white-matter-pathway alignment and tackles the long-standing issue in previous methods: the inability to recover the crossing fibers with high fidelity.

Integrated Construction of Multimodal Atlases with Structural Connectomes in the Space of Riemannian Metrics

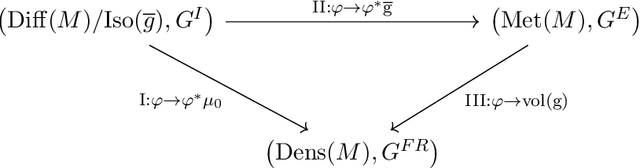
The structural network of the brain, or structural connectome, can be represented by fiber bundles generated by a variety of tractography methods. While such methods give qualitative insights into brain structure, there is controversy over whether they can provide quantitative information, especially at the population level. In order to enable population-level statistical analysis of the structural connectome, we propose representing a connectome as a Riemannian metric, which is a point on an infinite-dimensional manifold. We equip this manifold with the Ebin metric, a natural metric structure for this space, to get a Riemannian manifold along with its associated geometric properties. We then use this Riemannian framework to apply object-oriented statistical analysis to define an atlas as the Fr\'echet mean of a population of Riemannian metrics. This formulation ties into the existing framework for diffeomorphic construction of image atlases, allowing us to construct a multimodal atlas by simultaneously integrating complementary white matter structure details from DWMRI and cortical details from T1-weighted MRI. We illustrate our framework with 2D data examples of connectome registration and atlas formation. Finally, we build an example 3D multimodal atlas using T1 images and connectomes derived from diffusion tensors estimated from a subset of subjects from the Human Connectome Project.

Impact of Scene-Specific Enhancement Spectra on Matched Filter Greenhouse Gas Retrievals from Imaging Spectroscopy

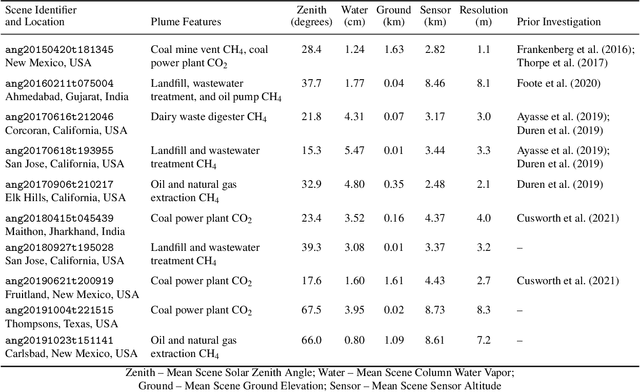
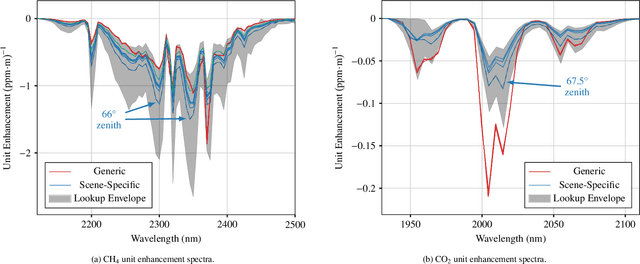
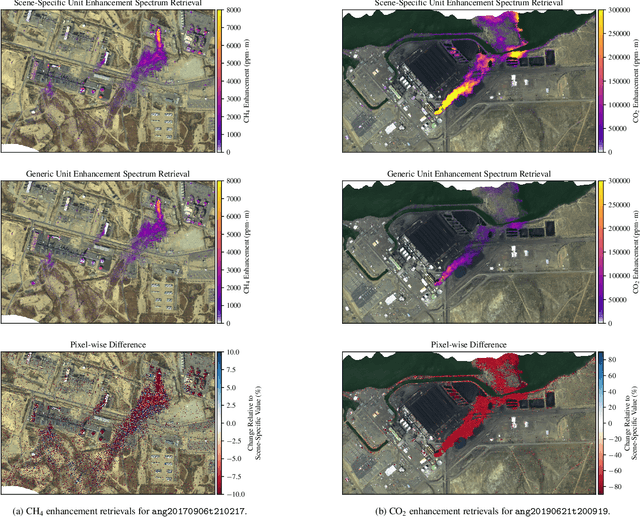
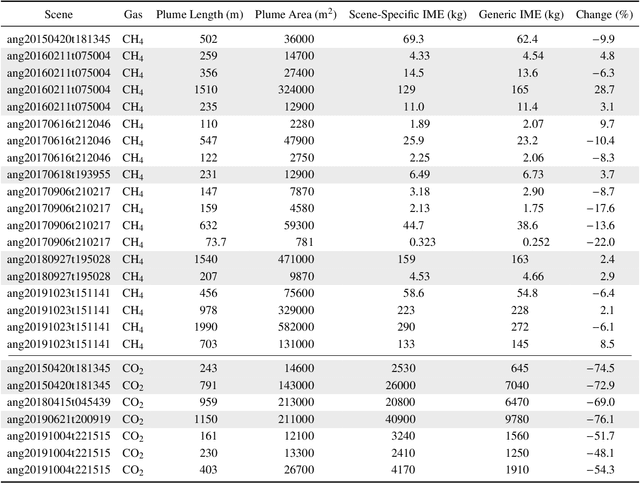
Matched filter (MF) techniques have been widely used for retrieval of greenhouse gas enhancements (enh.) from imaging spectroscopy datasets. While multiple algorithmic techniques and refinements have been proposed, the greenhouse gas target spectrum used for concentration enh. estimation has remained largely unaltered since the introduction of quantitative MF retrievals. The magnitude of retrieved methane and carbon dioxide enh., and thereby integrated mass enh. (IME) and estimated flux of point-source emitters, is heavily dependent on this target spectrum. Current standard use of molecular absorption coefficients to create unit enh. target spectra does not account for absorption by background concentrations of greenhouse gases, solar and sensor geometry, or atmospheric water vapor absorption. We introduce geometric and atmospheric parameters into the generation of scene-specific (SS) unit enh. spectra to provide target spectra that are compatible with all greenhouse gas retrieval MF techniques. For methane plumes, IME resulting from use of standard, generic enh. spectra varied from -22 to +28.7% compared to SS enh. spectra. Due to differences in spectral shape between the generic and SS enh. spectra, differences in methane plume IME were linked to surface spectral characteristics in addition to geometric and atmospheric parameters. IME differences for carbon dioxide plumes, with generic enh. spectra producing integrated mass enh. -76.1 to -48.1% compared to SS enh. spectra. Fluxes calculated from these integrated enh. would vary by the same %s, assuming equivalent wind conditions. Methane and carbon dioxide IME were most sensitive to changes in solar zenith angle and ground elevation. SS target spectra can improve confidence in greenhouse gas retrievals and flux estimates across collections of scenes with diverse geometric and atmospheric conditions.

Structural Connectome Atlas Construction in the Space of Riemannian Metrics

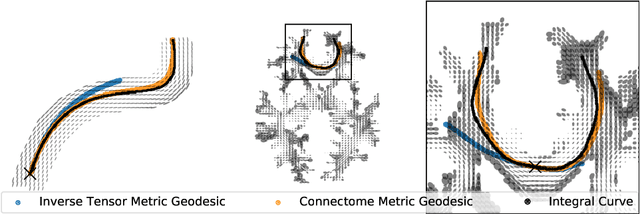
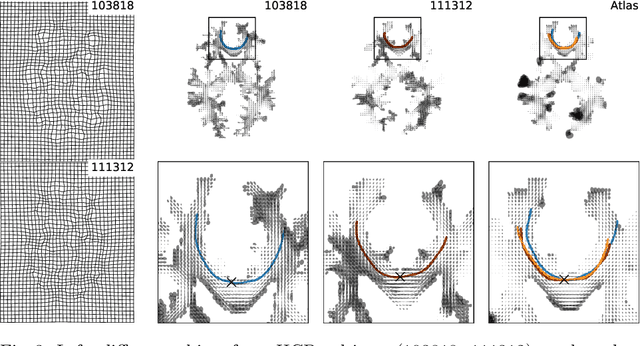
The structural connectome is often represented by fiber bundles generated from various types of tractography. We propose a method of analyzing connectomes by representing them as a Riemannian metric, thereby viewing them as points in an infinite-dimensional manifold. After equipping this space with a natural metric structure, the Ebin metric, we apply object-oriented statistical analysis to define an atlas as the Fr\'echet mean of a population of Riemannian metrics. We demonstrate connectome registration and atlas formation using connectomes derived from diffusion tensors estimated from a subset of subjects from the Human Connectome Project.