Deep Learning the Shape of the Brain Connectome

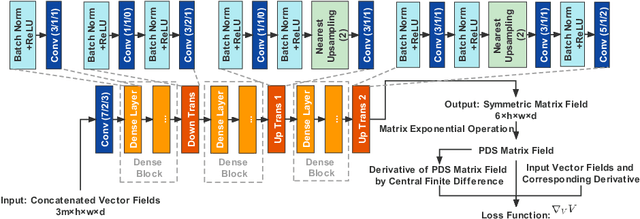
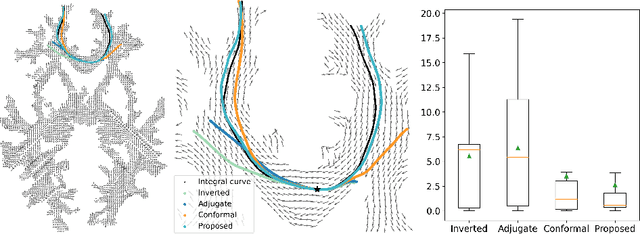
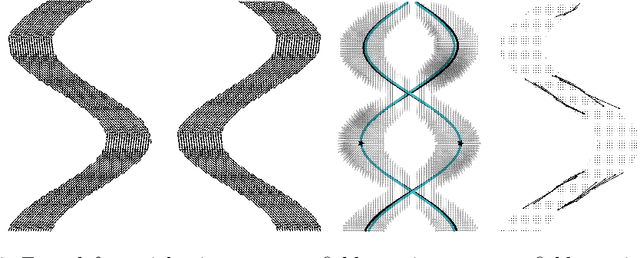
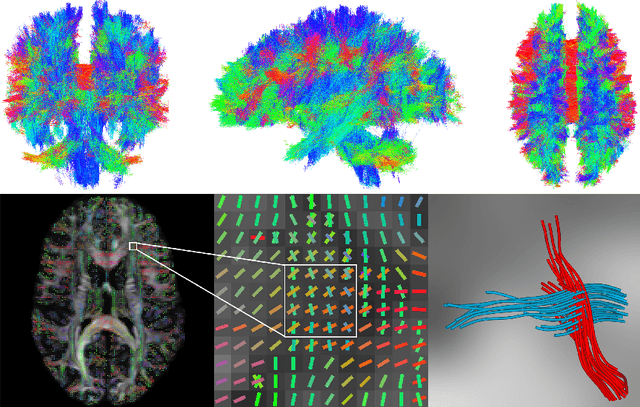
To statistically study the variability and differences between normal and abnormal brain connectomes, a mathematical model of the neural connections is required. In this paper, we represent the brain connectome as a Riemannian manifold, which allows us to model neural connections as geodesics. We show for the first time how one can leverage deep neural networks to estimate a Riemannian metric of the brain that can accommodate fiber crossings and is a natural modeling tool to infer the shape of the brain from DWMRI. Our method achieves excellent performance in geodesic-white-matter-pathway alignment and tackles the long-standing issue in previous methods: the inability to recover the crossing fibers with high fidelity.