Physics Informed Convex Artificial Neural Networks (PICANNs) for Optimal Transport based Density Estimation
Paper and Code
Apr 02, 2021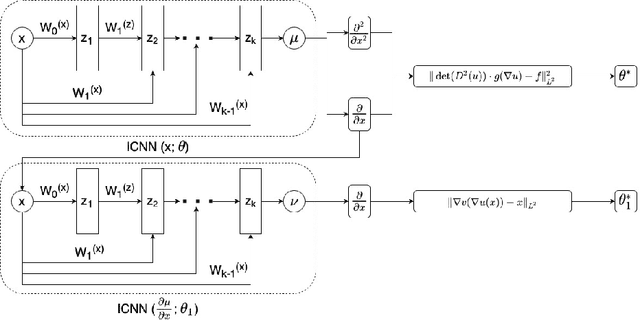

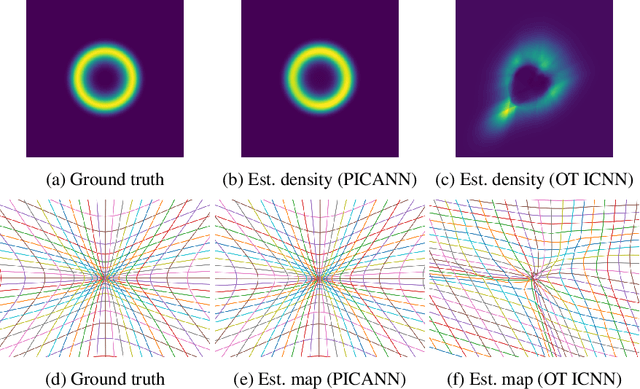
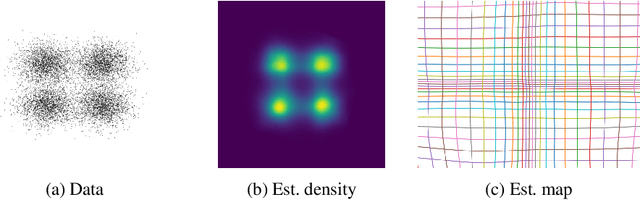
Optimal Mass Transport (OMT) is a well studied problem with a variety of applications in a diverse set of fields ranging from Physics to Computer Vision and in particular Statistics and Data Science. Since the original formulation of Monge in 1781 significant theoretical progress been made on the existence, uniqueness and properties of the optimal transport maps. The actual numerical computation of the transport maps, particularly in high dimensions, remains a challenging problem. By Brenier's theorem, the continuous OMT problem can be reduced to that of solving a non-linear PDE of Monge-Ampere type whose solution is a convex function. In this paper, building on recent developments of input convex neural networks and physics informed neural networks for solving PDE's, we propose a Deep Learning approach to solve the continuous OMT problem. To demonstrate the versatility of our framework we focus on the ubiquitous density estimation and generative modeling tasks in statistics and machine learning. Finally as an example we show how our framework can be incorporated with an autoencoder to estimate an effective probabilistic generative model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge