Adversarial Attack on Large Language Models using Exponentiated Gradient Descent

As Large Language Models (LLMs) are widely used, understanding them systematically is key to improving their safety and realizing their full potential. Although many models are aligned using techniques such as reinforcement learning from human feedback (RLHF), they are still vulnerable to jailbreaking attacks. Some of the existing adversarial attack methods search for discrete tokens that may jailbreak a target model while others try to optimize the continuous space represented by the tokens of the model's vocabulary. While techniques based on the discrete space may prove to be inefficient, optimization of continuous token embeddings requires projections to produce discrete tokens, which might render them ineffective. To fully utilize the constraints and the structures of the space, we develop an intrinsic optimization technique using exponentiated gradient descent with the Bregman projection method to ensure that the optimized one-hot encoding always stays within the probability simplex. We prove the convergence of the technique and implement an efficient algorithm that is effective in jailbreaking several widely used LLMs. We demonstrate the efficacy of the proposed technique using five open-source LLMs on four openly available datasets. The results show that the technique achieves a higher success rate with great efficiency compared to three other state-of-the-art jailbreaking techniques. The source code for our implementation is available at: https://github.com/sbamit/Exponentiated-Gradient-Descent-LLM-Attack

Mechanistic Understandings of Representation Vulnerabilities and Engineering Robust Vision Transformers

While transformer-based models dominate NLP and vision applications, their underlying mechanisms to map the input space to the label space semantically are not well understood. In this paper, we study the sources of known representation vulnerabilities of vision transformers (ViT), where perceptually identical images can have very different representations and semantically unrelated images can have the same representation. Our analysis indicates that imperceptible changes to the input can result in significant representation changes, particularly in later layers, suggesting potential instabilities in the performance of ViTs. Our comprehensive study reveals that adversarial effects, while subtle in early layers, propagate and amplify through the network, becoming most pronounced in middle to late layers. This insight motivates the development of NeuroShield-ViT, a novel defense mechanism that strategically neutralizes vulnerable neurons in earlier layers to prevent the cascade of adversarial effects. We demonstrate NeuroShield-ViT's effectiveness across various attacks, particularly excelling against strong iterative attacks, and showcase its remarkable zero-shot generalization capabilities. Without fine-tuning, our method achieves a competitive accuracy of 77.8% on adversarial examples, surpassing conventional robustness methods. Our results shed new light on how adversarial effects propagate through ViT layers, while providing a promising approach to enhance the robustness of vision transformers against adversarial attacks. Additionally, they provide a promising approach to enhance the robustness of vision transformers against adversarial attacks.

The Z-Gromov-Wasserstein Distance

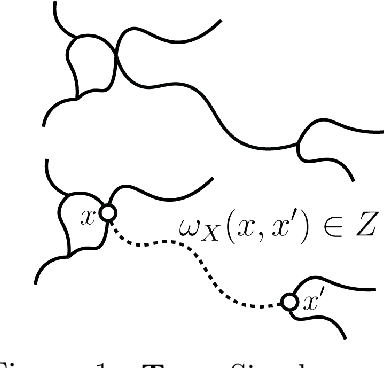
The Gromov-Wasserstein (GW) distance is a powerful tool for comparing metric measure spaces which has found broad applications in data science and machine learning. Driven by the need to analyze datasets whose objects have increasingly complex structure (such as node and edge-attributed graphs), several variants of GW distance have been introduced in the recent literature. With a view toward establishing a general framework for the theory of GW-like distances, this paper considers a vast generalization of the notion of a metric measure space: for an arbitrary metric space $Z$, we define a $Z$-network to be a measure space endowed with a kernel valued in $Z$. We introduce a method for comparing $Z$-networks by defining a generalization of GW distance, which we refer to as $Z$-Gromov-Wasserstein ($Z$-GW) distance. This construction subsumes many previously known metrics and offers a unified approach to understanding their shared properties. The paper demonstrates that the $Z$-GW distance defines a metric on the space of $Z$-networks which retains desirable properties of $Z$, such as separability, completeness, and geodesicity. Many of these properties were unknown for existing variants of GW distance that fall under our framework. Our focus is on foundational theory, but our results also include computable lower bounds and approximations of the distance which will be useful for practical applications.