Matching aggregate posteriors in the variational autoencoder
Paper and Code
Nov 13, 2023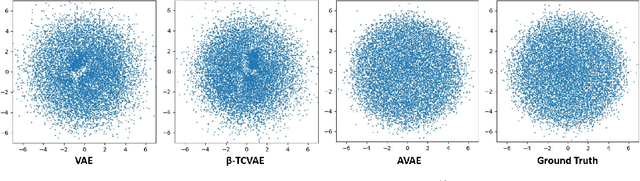

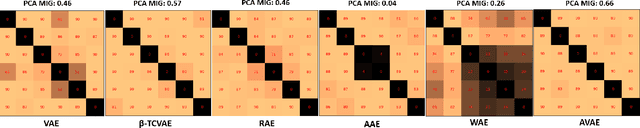
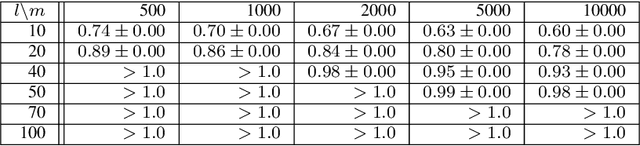
The variational autoencoder (VAE) is a well-studied, deep, latent-variable model (DLVM) that efficiently optimizes the variational lower bound of the log marginal data likelihood and has a strong theoretical foundation. However, the VAE's known failure to match the aggregate posterior often results in \emph{pockets/holes} in the latent distribution (i.e., a failure to match the prior) and/or \emph{posterior collapse}, which is associated with a loss of information in the latent space. This paper addresses these shortcomings in VAEs by reformulating the objective function associated with VAEs in order to match the aggregate/marginal posterior distribution to the prior. We use kernel density estimate (KDE) to model the aggregate posterior in high dimensions. The proposed method is named the \emph{aggregate variational autoencoder} (AVAE) and is built on the theoretical framework of the VAE. Empirical evaluation of the proposed method on multiple benchmark data sets demonstrates the effectiveness of the AVAE relative to state-of-the-art (SOTA) methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge