Unbiasing Procedures for Scale-invariant Multi-reference Alignment
Paper and Code
Jul 02, 2021

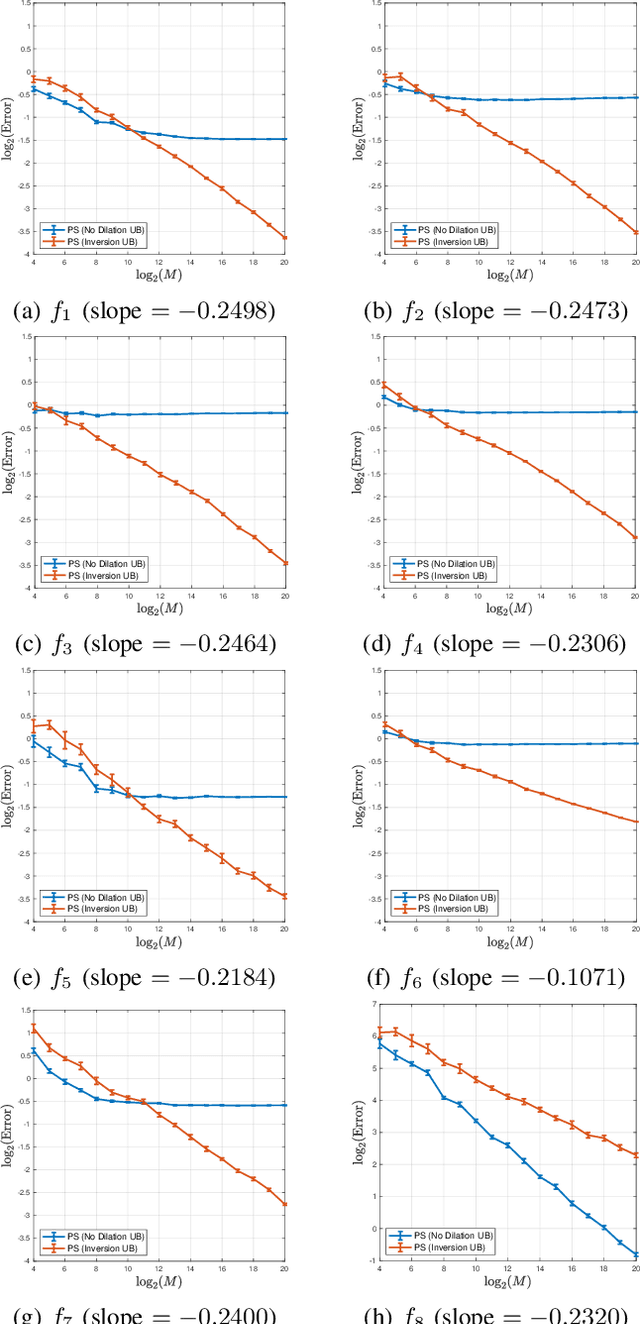
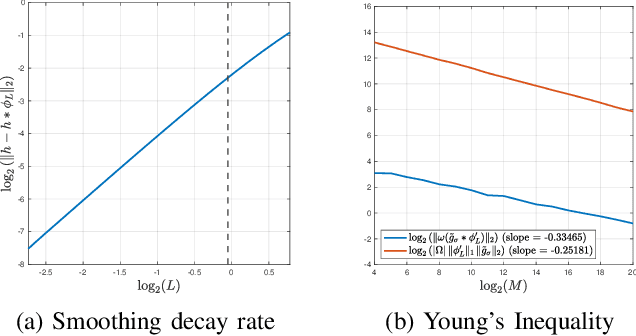
This article discusses a generalization of the 1-dimensional multi-reference alignment problem. The goal is to recover a hidden signal from many noisy observations, where each noisy observation includes a random translation and random dilation of the hidden signal, as well as high additive noise. We propose a method that recovers the power spectrum of the hidden signal by applying a data-driven, nonlinear unbiasing procedure, and thus the hidden signal is obtained up to an unknown phase. An unbiased estimator of the power spectrum is defined, whose error depends on the sample size and noise levels, and we precisely quantify the convergence rate of the proposed estimator. The unbiasing procedure relies on knowledge of the dilation distribution, and we implement an optimization procedure to learn the dilation variance when this parameter is unknown. Our theoretical work is supported by extensive numerical experiments on a wide range of signals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge