Taxonomy of Benchmarks in Graph Representation Learning

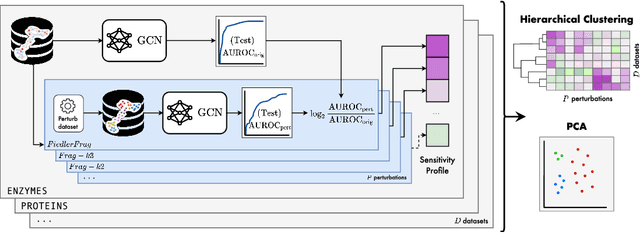
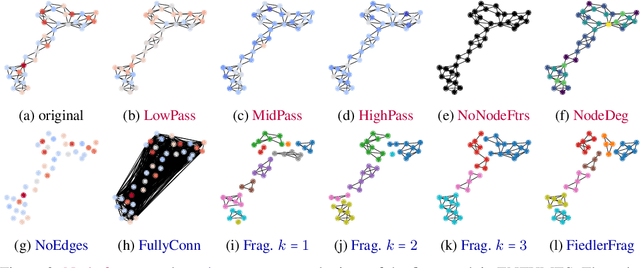
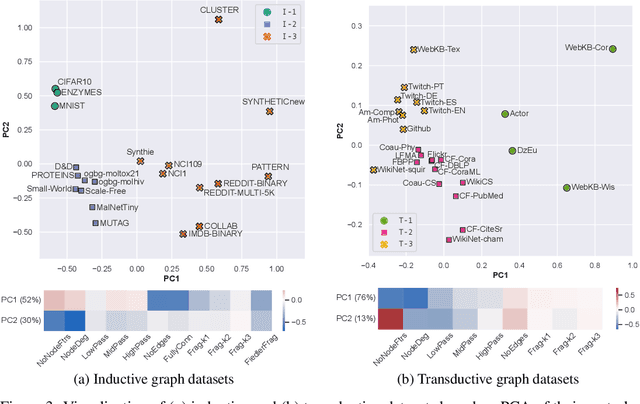
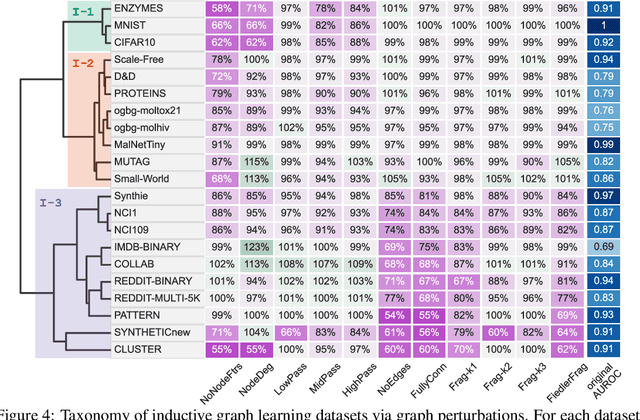
Graph Neural Networks (GNNs) extend the success of neural networks to graph-structured data by accounting for their intrinsic geometry. While extensive research has been done on developing GNN models with superior performance according to a collection of graph representation learning benchmarks, it is currently not well understood what aspects of a given model are probed by them. For example, to what extent do they test the ability of a model to leverage graph structure vs. node features? Here, we develop a principled approach to taxonomize benchmarking datasets according to a $\textit{sensitivity profile}$ that is based on how much GNN performance changes due to a collection of graph perturbations. Our data-driven analysis provides a deeper understanding of which benchmarking data characteristics are leveraged by GNNs. Consequently, our taxonomy can aid in selection and development of adequate graph benchmarks, and better informed evaluation of future GNN methods. Finally, our approach and implementation in $\texttt{GTaxoGym}$ package are extendable to multiple graph prediction task types and future datasets.

Towards a Taxonomy of Graph Learning Datasets

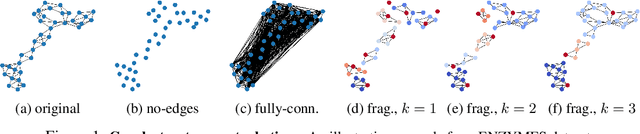
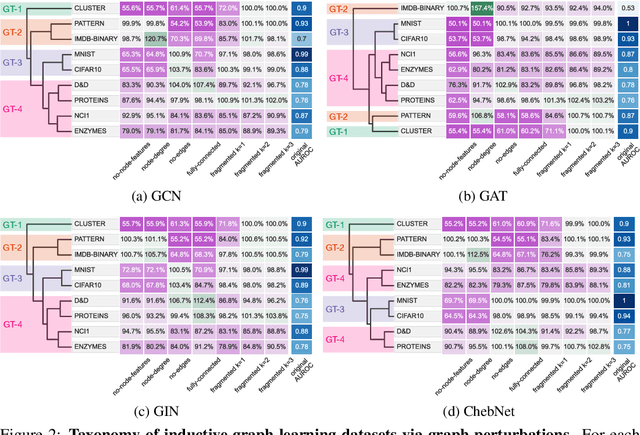
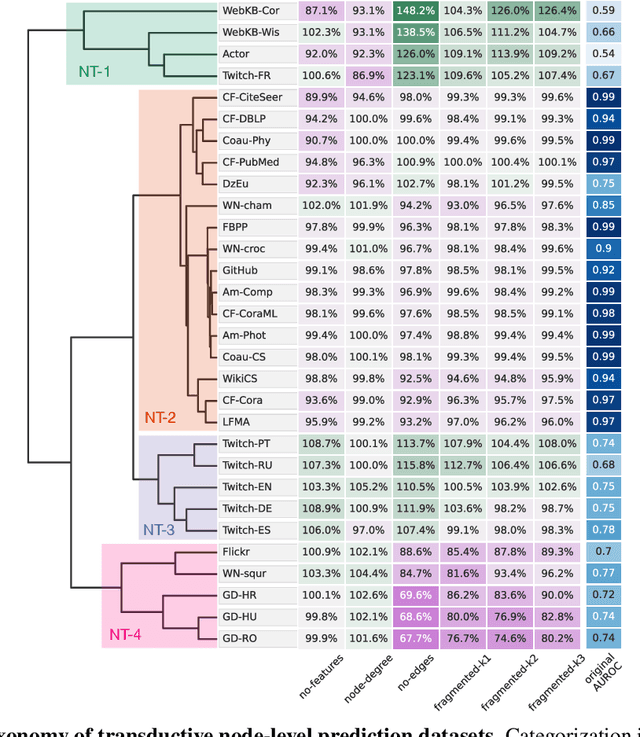
Graph neural networks (GNNs) have attracted much attention due to their ability to leverage the intrinsic geometries of the underlying data. Although many different types of GNN models have been developed, with many benchmarking procedures to demonstrate the superiority of one GNN model over the others, there is a lack of systematic understanding of the underlying benchmarking datasets, and what aspects of the model are being tested. Here, we provide a principled approach to taxonomize graph benchmarking datasets by carefully designing a collection of graph perturbations to probe the essential data characteristics that GNN models leverage to perform predictions. Our data-driven taxonomization of graph datasets provides a new understanding of critical dataset characteristics that will enable better model evaluation and the development of more specialized GNN models.

Rethinking Graph Transformers with Spectral Attention

In recent years, the Transformer architecture has proven to be very successful in sequence processing, but its application to other data structures, such as graphs, has remained limited due to the difficulty of properly defining positions. Here, we present the $\textit{Spectral Attention Network}$ (SAN), which uses a learned positional encoding (LPE) that can take advantage of the full Laplacian spectrum to learn the position of each node in a given graph. This LPE is then added to the node features of the graph and passed to a fully-connected Transformer. By leveraging the full spectrum of the Laplacian, our model is theoretically powerful in distinguishing graphs, and can better detect similar sub-structures from their resonance. Further, by fully connecting the graph, the Transformer does not suffer from over-squashing, an information bottleneck of most GNNs, and enables better modeling of physical phenomenons such as heat transfer and electric interaction. When tested empirically on a set of 4 standard datasets, our model performs on par or better than state-of-the-art GNNs, and outperforms any attention-based model by a wide margin, becoming the first fully-connected architecture to perform well on graph benchmarks.