Graph Positional and Structural Encoder

Positional and structural encodings (PSE) enable better identifiability of nodes within a graph, as in general graphs lack a canonical node ordering. This renders PSEs essential tools for empowering modern GNNs, and in particular graph Transformers. However, designing PSEs that work optimally for a variety of graph prediction tasks is a challenging and unsolved problem. Here, we present the graph positional and structural encoder (GPSE), a first-ever attempt to train a graph encoder that captures rich PSE representations for augmenting any GNN. GPSE can effectively learn a common latent representation for multiple PSEs, and is highly transferable. The encoder trained on a particular graph dataset can be used effectively on datasets drawn from significantly different distributions and even modalities. We show that across a wide range of benchmarks, GPSE-enhanced models can significantly improve the performance in certain tasks, while performing on par with those that employ explicitly computed PSEs in other cases. Our results pave the way for the development of large pre-trained models for extracting graph positional and structural information and highlight their potential as a viable alternative to explicitly computed PSEs as well as to existing self-supervised pre-training approaches.

Rethinking Graph Transformers with Spectral Attention

In recent years, the Transformer architecture has proven to be very successful in sequence processing, but its application to other data structures, such as graphs, has remained limited due to the difficulty of properly defining positions. Here, we present the $\textit{Spectral Attention Network}$ (SAN), which uses a learned positional encoding (LPE) that can take advantage of the full Laplacian spectrum to learn the position of each node in a given graph. This LPE is then added to the node features of the graph and passed to a fully-connected Transformer. By leveraging the full spectrum of the Laplacian, our model is theoretically powerful in distinguishing graphs, and can better detect similar sub-structures from their resonance. Further, by fully connecting the graph, the Transformer does not suffer from over-squashing, an information bottleneck of most GNNs, and enables better modeling of physical phenomenons such as heat transfer and electric interaction. When tested empirically on a set of 4 standard datasets, our model performs on par or better than state-of-the-art GNNs, and outperforms any attention-based model by a wide margin, becoming the first fully-connected architecture to perform well on graph benchmarks.

Directional Graph Networks

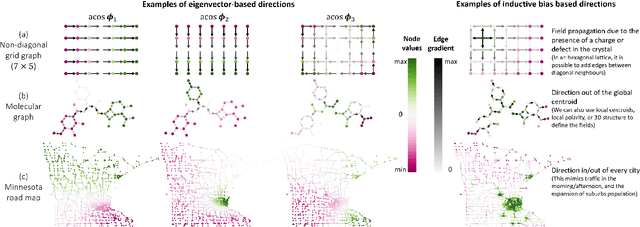
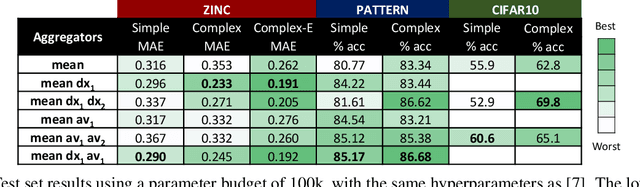
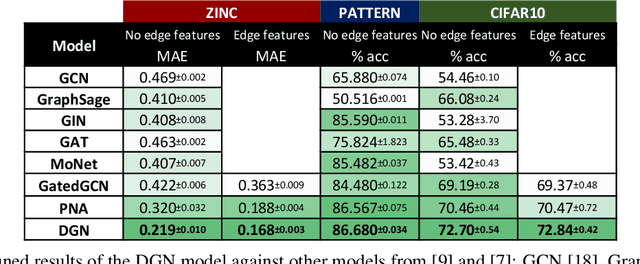
In order to overcome the expressive limitations of graph neural networks (GNNs), we propose the first method that exploits vector flows over graphs to develop globally consistent directional and asymmetric aggregation functions. We show that our directional graph networks (DGNs) generalize convolutional neural networks (CNNs) when applied on a grid. Whereas recent theoretical works focus on understanding local neighbourhoods, local structures and local isomorphism with no global information flow, our novel theoretical framework allows directional convolutional kernels in any graph. First, by defining a vector field in the graph, we develop a method of applying directional derivatives and smoothing by projecting node-specific messages into the field. Then we propose the use of the Laplacian eigenvectors as such vector field, and we show that the method generalizes CNNs on an n-dimensional grid. Finally, we bring the power of CNN data augmentation to graphs by providing a means of doing reflection, rotation and distortion on the underlying directional field. We evaluate our method on different standard benchmarks and see a relative error reduction of 8% on the CIFAR10 graph dataset and 11% to 32% on the molecular ZINC dataset. An important outcome of this work is that it enables to translate any physical or biological problems with intrinsic directional axes into a graph network formalism with an embedded directional field.