Path-Based Spectral Clustering: Guarantees, Robustness to Outliers, and Fast Algorithms
Paper and Code
Dec 17, 2017
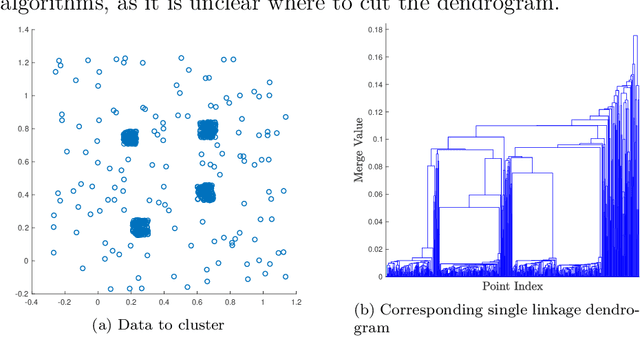
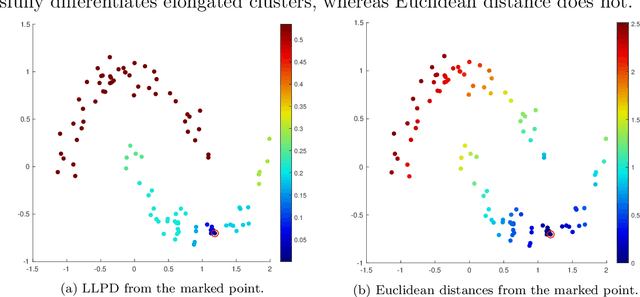
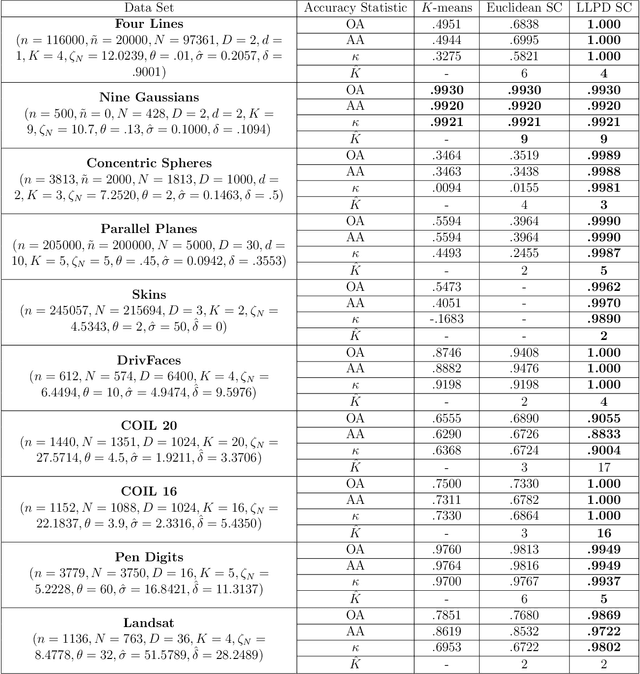
We consider the problem of clustering with the longest leg path distance (LLPD) metric, which is informative for elongated and irregularly shaped clusters. We prove finite-sample guarantees on the performance of clustering with respect to this metric when random samples are drawn from multiple intrinsically low-dimensional clusters in high-dimensional space, in the presence of a large number of high-dimensional outliers. By combining these results with spectral clustering with respect to LLPD, we provide conditions under which the eigengap statistic correctly determines the number of clusters for a large class of data sets, and prove guarantees on the number of points mislabeled by the proposed algorithm. Our methods are quite general and provide performance guarantees for spectral clustering with any ultrametric. We also introduce an efficient approximation algorithm, easy to implement, for the LLPD, based on a multiscale analysis of adjacency graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge