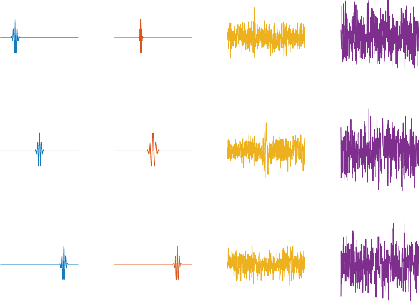
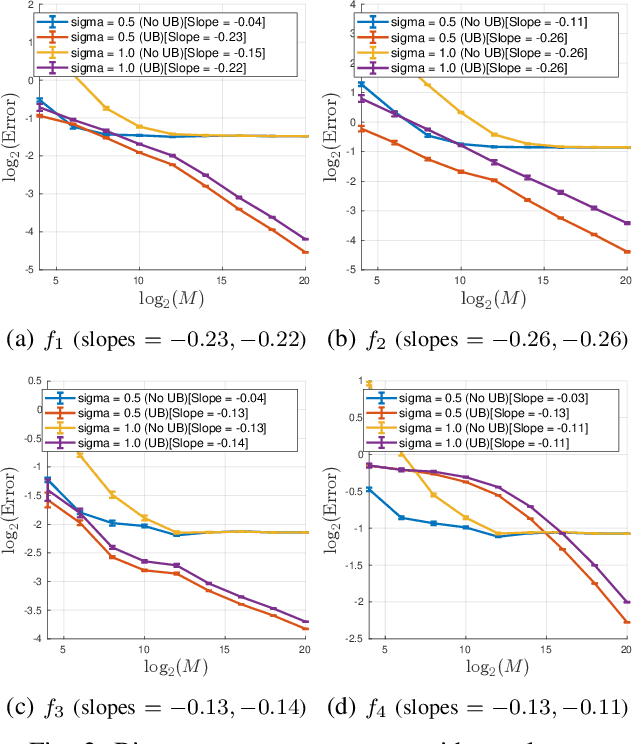
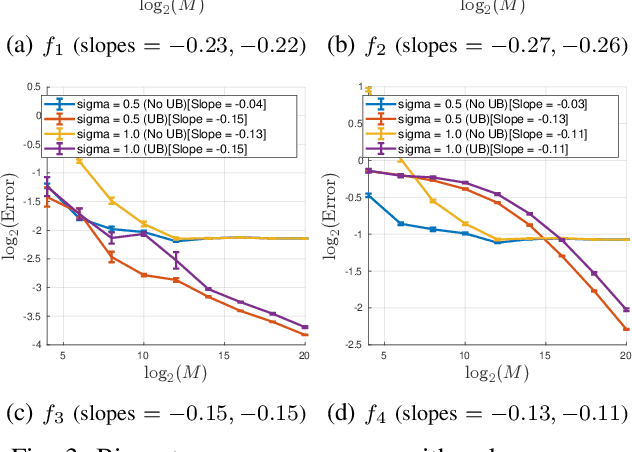
Bispectrum Unbiasing for Dilation-Invariant Multi-reference Alignment

Motivated by modern data applications such as cryo-electron microscopy, the goal of classic multi-reference alignment (MRA) is to recover an unknown signal $f: \mathbb{R} \to \mathbb{R}$ from many observations that have been randomly translated and corrupted by additive noise. We consider a generalization of classic MRA where signals are also corrupted by a random scale change, i.e. dilation. We propose a novel data-driven unbiasing procedure which can recover an unbiased estimator of the bispectrum of the unknown signal, given knowledge of the dilation distribution. Lastly, we invert the recovered bispectrum to achieve full signal recovery, and validate our methodology on a set of synthetic signals.

Long Range Constraints for Neural Texture Synthesis Using Sliced Wasserstein Loss

In the past decade, exemplar-based texture synthesis algorithms have seen strong gains in performance by matching statistics of deep convolutional neural networks. However, these algorithms require regularization terms or user-added spatial tags to capture long range constraints in images. Having access to a user-added spatial tag for all situations is not always feasible, and regularization terms can be difficult to tune. It would be ideal to create an algorithm that does not have any of the aforementioned drawbacks. Thus, we propose a new set of statistics for exemplar based texture synthesis based on Sliced Wasserstein Loss and create a multi-scale algorithm to synthesize textures without a user-added spatial tag. Lastly, we study the ability of our proposed algorithm to capture long range constraints in images and compare our results to other exemplar-based neural texture synthesis algorithms.