Using persistent homology to understand dimensionality reduction in resting-state fMRI

Evaluating the success of a manifold learning method remains a challenging problem, especially for methods adapted to a specific application domain. The present work investigates shared geometric structure across different dimensionality reduction (DR) algorithms within the scope of neuroimaging applications. We examine reduced-dimension embeddings produced by a representative assay of dimension reductions for brain data ("brain representations") through the lens of persistent homology, making statistical claims about topological differences using a recent topological boostrap method. We cluster these methods based on their induced topologies, finding feature type and number -- rather than reduction algorithm -- as the main drivers of observed topological differences.

NervePool: A Simplicial Pooling Layer

For deep learning problems on graph-structured data, pooling layers are important for down sampling, reducing computational cost, and to minimize overfitting. We define a pooling layer, NervePool, for data structured as simplicial complexes, which are generalizations of graphs that include higher-dimensional simplices beyond vertices and edges; this structure allows for greater flexibility in modeling higher-order relationships. The proposed simplicial coarsening scheme is built upon partitions of vertices, which allow us to generate hierarchical representations of simplicial complexes, collapsing information in a learned fashion. NervePool builds on the learned vertex cluster assignments and extends to coarsening of higher dimensional simplices in a deterministic fashion. While in practice, the pooling operations are computed via a series of matrix operations, the topological motivation is a set-theoretic construction based on unions of stars of simplices and the nerve complex

Robust Zero-crossings Detection in Noisy Signals using Topological Signal Processing

We explore a novel application of zero-dimensional persistent homology from Topological Data Analysis (TDA) for bracketing zero-crossings of both one-dimensional continuous functions, and uniformly sampled time series. We present an algorithm and show its robustness in the presence of noise for a range of sampling frequencies. In comparison to state-of-the-art software-based methods for finding zeros of a time series, our method generally converges faster, provides higher accuracy, and is capable of finding all the roots in a given interval instead of converging only to one of them. We also present and compare options for automatically setting the persistence threshold parameter that influences the accurate bracketing of the roots.

Automatic Tree Ring Detection using Jacobi Sets

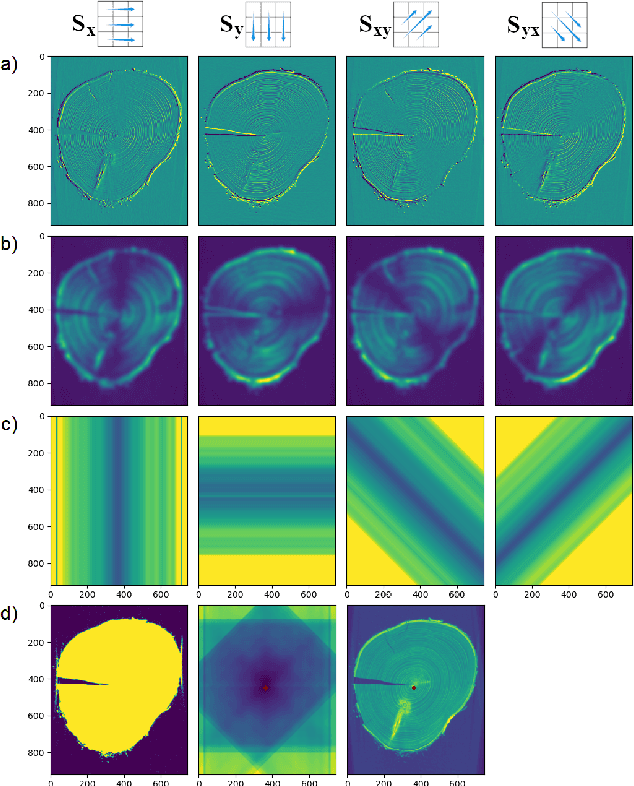
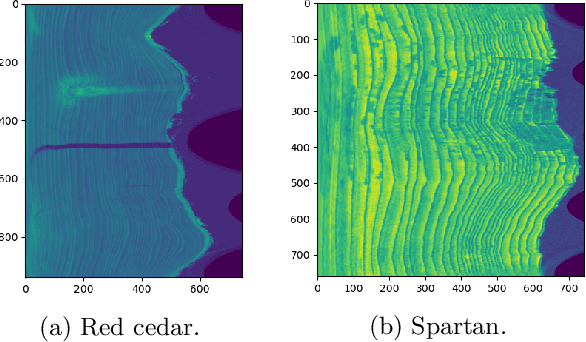
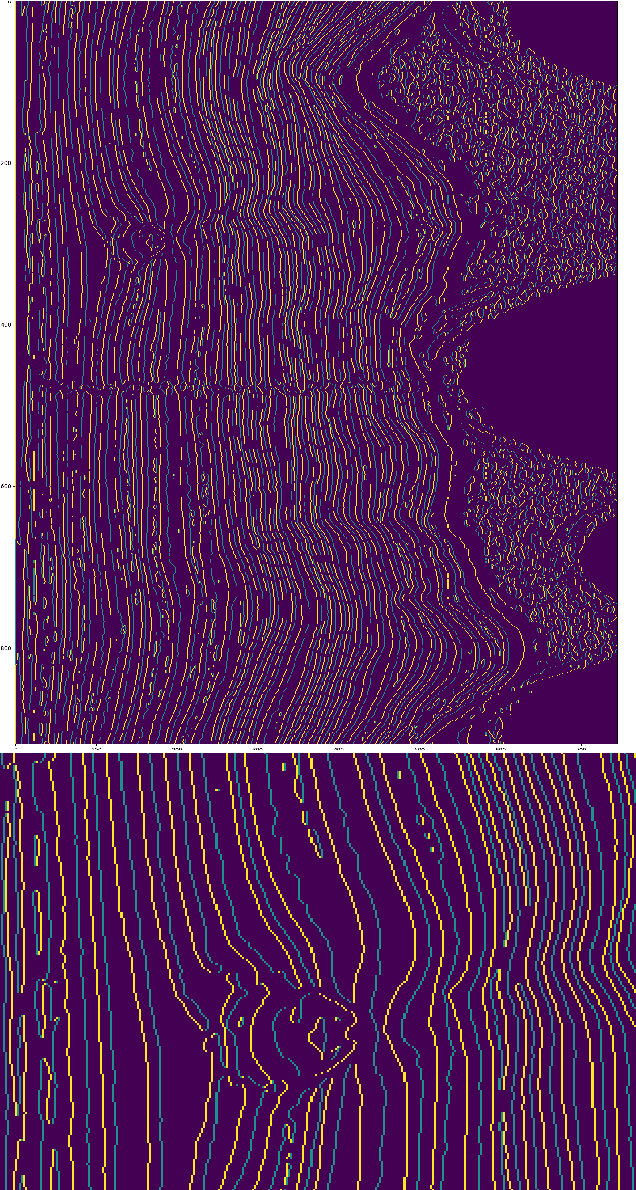
Tree ring widths are an important source of climatic and historical data, but measuring these widths typically requires extensive manual work. Computer vision techniques provide promising directions towards the automation of tree ring detection, but most automated methods still require a substantial amount of user interaction to obtain high accuracy. We perform analysis on 3D X-ray CT images of a cross-section of a tree trunk, known as a tree disk. We present novel automated methods for locating the pith (center) of a tree disk, and ring boundaries. Our methods use a combination of standard image processing techniques and tools from topological data analysis. We evaluate the efficacy of our method for two different CT scans by comparing its results to manually located rings and centers and show that it is better than current automatic methods in terms of correctly counting each ring and its location. Our methods have several parameters, which we optimize experimentally by minimizing edit distances to the manually obtained locations.

Graph Similarity Using PageRank and Persistent Homology

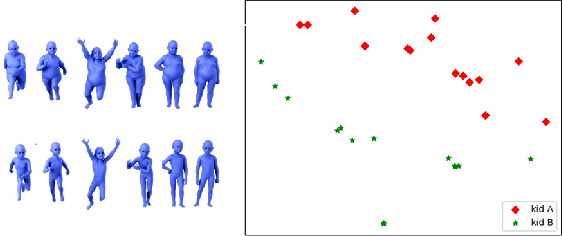
The PageRank of a graph is a scalar function defined on the node set of the graph which encodes nodes centrality information of the graph. In this work, we utilize the PageRank function on the lower-star filtration of the graph as input to persistent homology to study the problem of graph similarity. By representing each graph as a persistence diagram, we can then compare outputs using the bottleneck distance. We show the effectiveness of our method by utilizing it on two shape mesh datasets.

Chatter Diagnosis in Milling Using Supervised Learning and Topological Features Vector

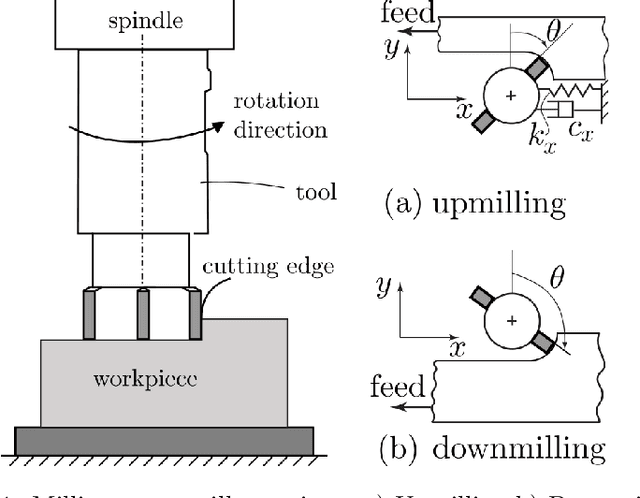
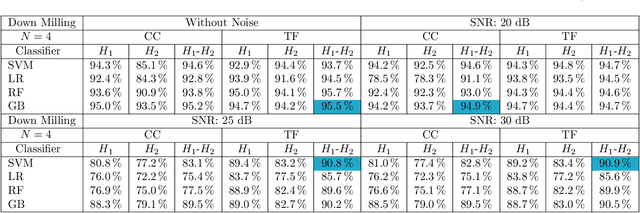
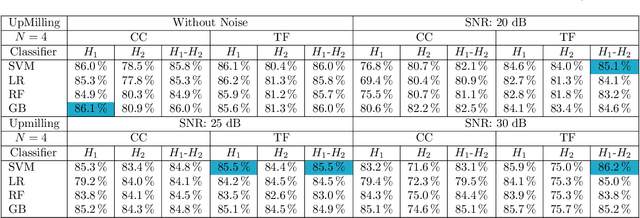
Chatter detection has become a prominent subject of interest due to its effect on cutting tool life, surface finish and spindle of machine tool. Most of the existing methods in chatter detection literature are based on signal processing and signal decomposition. In this study, we use topological features of data simulating cutting tool vibrations, combined with four supervised machine learning algorithms to diagnose chatter in the milling process. Persistence diagrams, a method of representing topological features, are not easily used in the context of machine learning, so they must be transformed into a form that is more amenable. Specifically, we will focus on two different methods for featurizing persistence diagrams, Carlsson coordinates and template functions. In this paper, we provide classification results for simulated data from various cutting configurations, including upmilling and downmilling, in addition to the same data with some added noise. Our results show that Carlsson Coordinates and Template Functions yield accuracies as high as 96% and 95%, respectively. We also provide evidence that these topological methods are noise robust descriptors for chatter detection.

Adaptive Partitioning for Template Functions on Persistence Diagrams

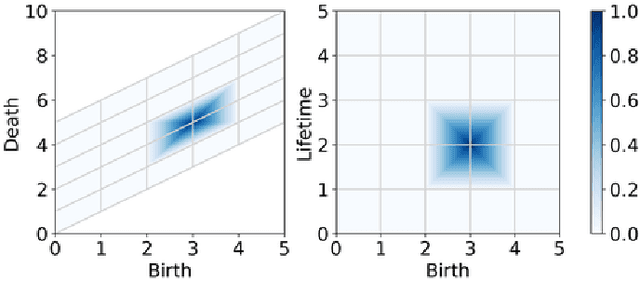
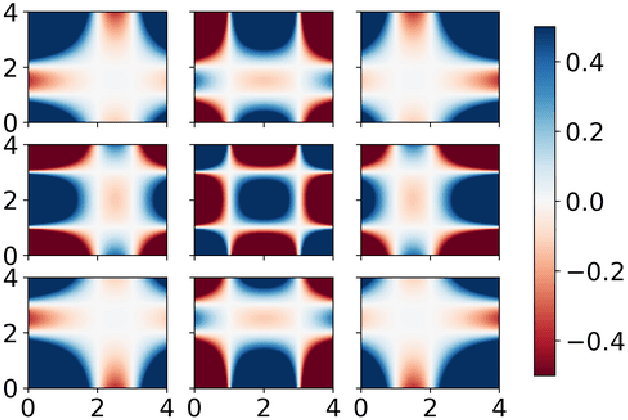
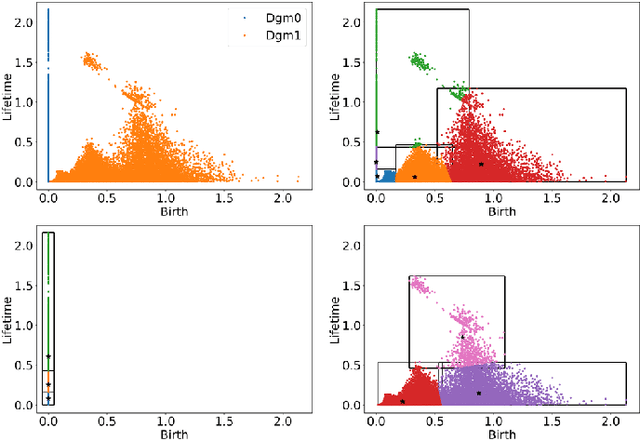
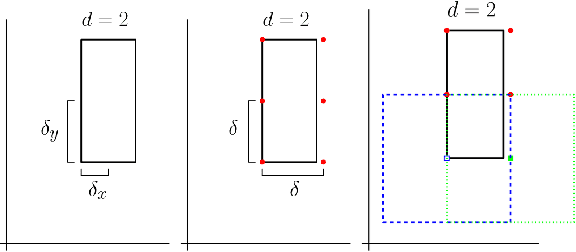
As the field of Topological Data Analysis continues to show success in theory and in applications, there has been increasing interest in using tools from this field with methods for machine learning. Using persistent homology, specifically persistence diagrams, as inputs to machine learning techniques requires some mathematical creativity. The space of persistence diagrams does not have the desirable properties for machine learning, thus methods such as kernel methods and vectorization methods have been developed. One such featurization of persistence diagrams by Perea, Munch and Khasawneh uses continuous, compactly supported functions, referred to as "template functions," which results in a stable vector representation of the persistence diagram. In this paper, we provide a method of adaptively partitioning persistence diagrams to improve these featurizations based on localized information in the diagrams. Additionally, we provide a framework to adaptively select parameters required for the template functions in order to best utilize the partitioning method. We present results for application to example data sets comparing classification results between template function featurizations with and without partitioning, in addition to other methods from the literature.

Approximating Continuous Functions on Persistence Diagrams Using Template Functions

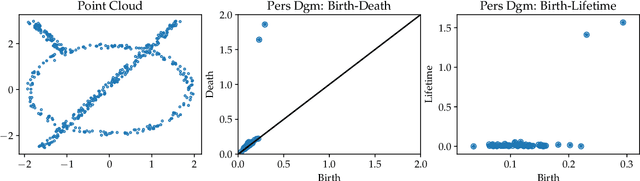
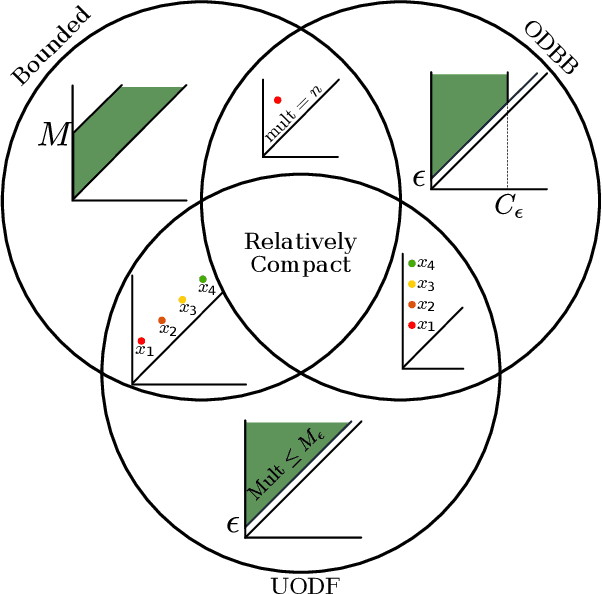
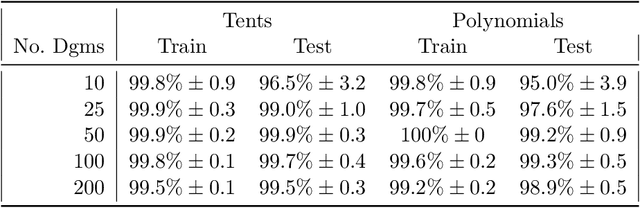
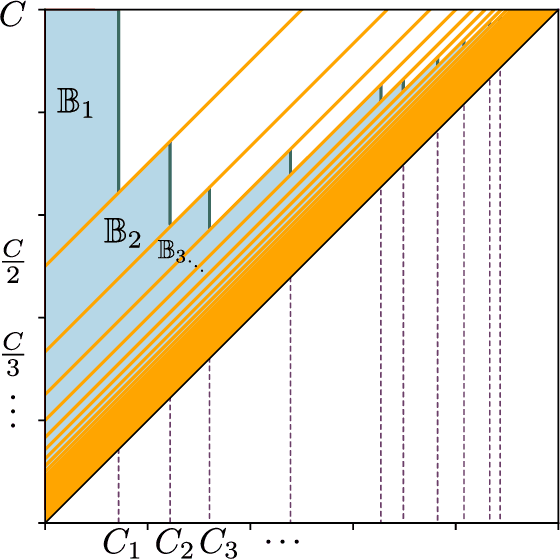
The persistence diagram is an increasingly useful tool from Topological Data Analysis, but its use alongside typical machine learning techniques requires mathematical finesse. The most success to date has come from methods that map persistence diagrams into $\mathbb{R}^n$, in a way which maximizes the structure preserved. This process is commonly referred to as featurization. In this paper, we describe a mathematical framework for featurization using template functions. These functions are general as they are only required to be continuous and compactly supported. We discuss two realizations: tent functions, which emphasize the local contributions of points in a persistence diagram, and interpolating polynomials, which capture global pairwise interactions. We combine the resulting features with classification and regression algorithms on several examples including shape data and the Rossler system. Our results show that using template functions yields high accuracy rates that match and often exceed those of existing featurization methods. One counter-intuitive observation is that in most cases using interpolating polynomials, where each point contributes globally to the feature vector, yields significantly better results than using tent functions, where the contribution of each point is localized. Along the way, we provide a complete characterization of compactness in the space of persistence diagrams.

Using Persistent Homology to Quantify a Diurnal Cycle in Hurricane Felix

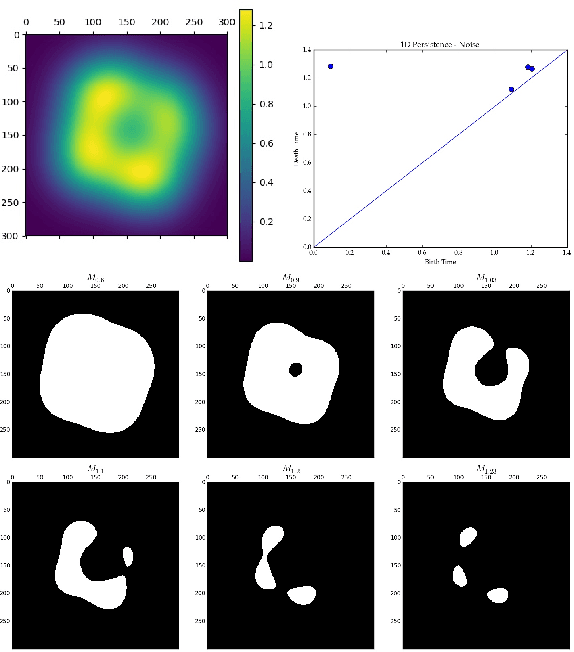
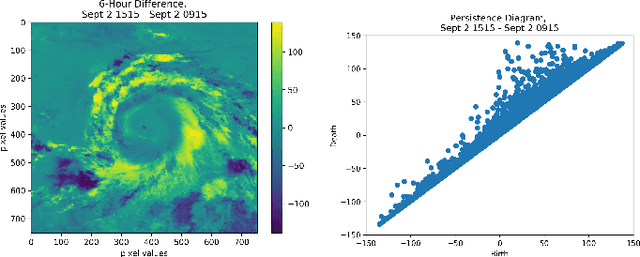
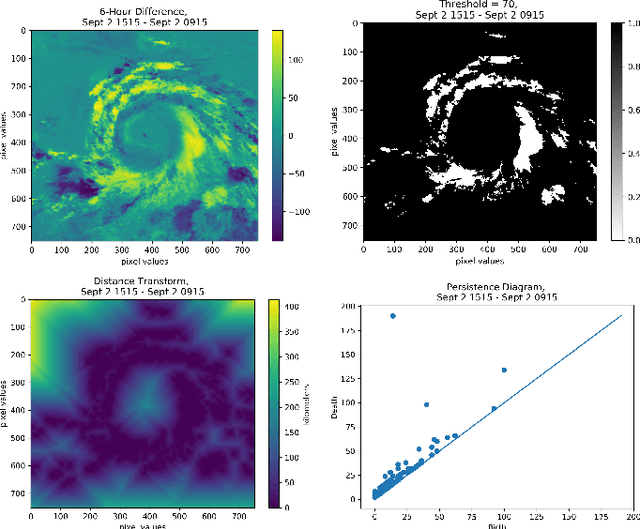
The diurnal cycle of tropical cyclones (TCs) is a daily cycle in clouds that appears in satellite images and may have implications for TC structure and intensity. The diurnal pattern can be seen in infrared (IR) satellite imagery as cyclical pulses in the cloud field that propagate radially outward from the center of nearly all Atlantic-basin TCs. These diurnal pulses, a distinguishing characteristic of the TC diurnal cycle, begin forming in the storm's inner core near sunset each day and appear as a region of cooling cloud-top temperatures. The area of cooling takes on a ring-like appearance as cloud-top warming occurs on its inside edge and the cooling moves away from the storm overnight, reaching several hundred kilometers from the circulation center by the following afternoon. The state-of-the-art TC diurnal cycle measurement has a limited ability to analyze the behavior beyond qualitative observations. We present a method for quantifying the TC diurnal cycle using one-dimensional persistent homology, a tool from Topological Data Analysis, by tracking maximum persistence and quantifying the cycle using the discrete Fourier transform. Using Geostationary Operational Environmental Satellite IR imagery data from Hurricane Felix (2007), our method is able to detect an approximate daily cycle.

Chatter Classification in Turning Using Machine Learning and Topological Data Analysis

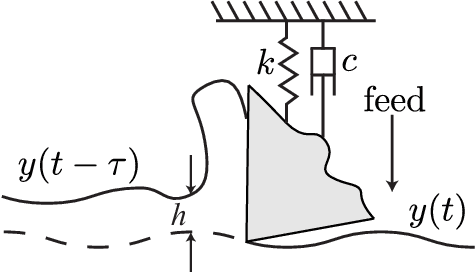
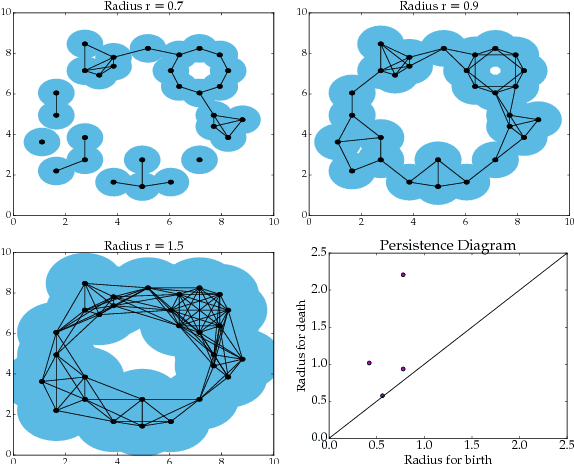
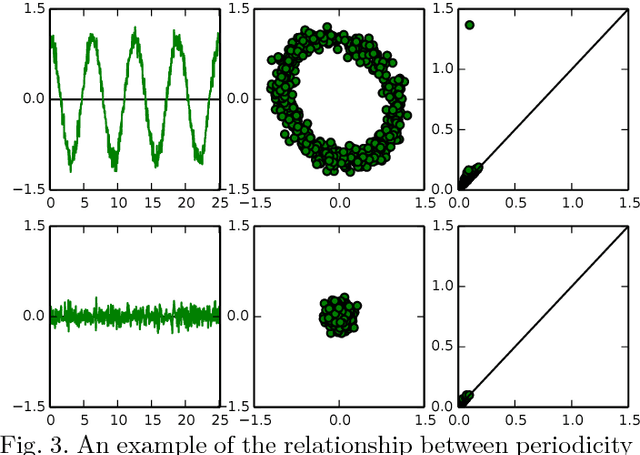
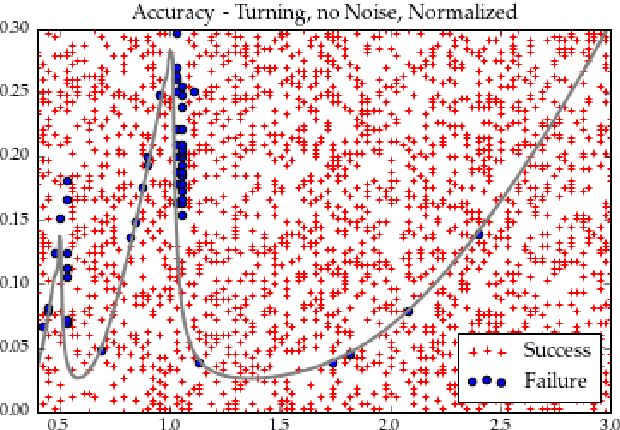
Chatter identification and detection in machining processes has been an active area of research in the past two decades. Part of the challenge in studying chatter is that machining equations that describe its occurrence are often nonlinear delay differential equations. The majority of the available tools for chatter identification rely on defining a metric that captures the characteristics of chatter, and a threshold that signals its occurrence. The difficulty in choosing these parameters can be somewhat alleviated by utilizing machine learning techniques. However, even with a successful classification algorithm, the transferability of typical machine learning methods from one data set to another remains very limited. In this paper we combine supervised machine learning with Topological Data Analysis (TDA) to obtain a descriptor of the process which can detect chatter. The features we use are derived from the persistence diagram of an attractor reconstructed from the time series via Takens embedding. We test the approach using deterministic and stochastic turning models, where the stochasticity is introduced via the cutting coefficient term. Our results show a 97% successful classification rate on the deterministic model labeled by the stability diagram obtained using the spectral element method. The features gleaned from the deterministic model are then utilized for characterization of chatter in a stochastic turning model where there are very limited analysis methods.