Topological Signatures of ReLU Neural Network Activation Patterns

This paper explores the topological signatures of ReLU neural network activation patterns. We consider feedforward neural networks with ReLU activation functions and analyze the polytope decomposition of the feature space induced by the network. Mainly, we investigate how the Fiedler partition of the dual graph and show that it appears to correlate with the decision boundary -- in the case of binary classification. Additionally, we compute the homology of the cellular decomposition -- in a regression task -- to draw similar patterns in behavior between the training loss and polyhedral cell-count, as the model is trained.

Topological Detection of Phenomenological Bifurcations with Unreliable Kernel Densities

Phenomenological (P-type) bifurcations are qualitative changes in stochastic dynamical systems whereby the stationary probability density function (PDF) changes its topology. The current state of the art for detecting these bifurcations requires reliable kernel density estimates computed from an ensemble of system realizations. However, in several real world signals such as Big Data, only a single system realization is available -- making it impossible to estimate a reliable kernel density. This study presents an approach for detecting P-type bifurcations using unreliable density estimates. The approach creates an ensemble of objects from Topological Data Analysis (TDA) called persistence diagrams from the system's sole realization and statistically analyzes the resulting set. We compare several methods for replicating the original persistence diagram including Gibbs point process modelling, Pairwise Interaction Point Modelling, and subsampling. We show that for the purpose of predicting a bifurcation, the simple method of subsampling exceeds the other two methods of point process modelling in performance.

Robust Zero-crossings Detection in Noisy Signals using Topological Signal Processing

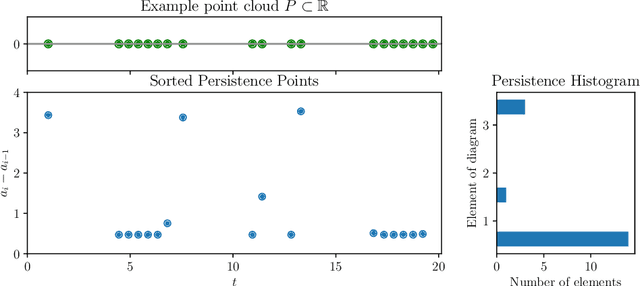
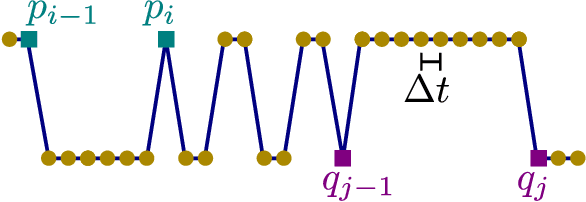
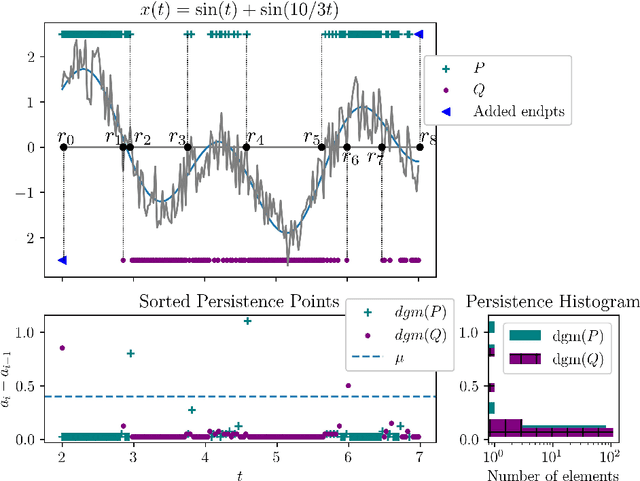
We explore a novel application of zero-dimensional persistent homology from Topological Data Analysis (TDA) for bracketing zero-crossings of both one-dimensional continuous functions, and uniformly sampled time series. We present an algorithm and show its robustness in the presence of noise for a range of sampling frequencies. In comparison to state-of-the-art software-based methods for finding zeros of a time series, our method generally converges faster, provides higher accuracy, and is capable of finding all the roots in a given interval instead of converging only to one of them. We also present and compare options for automatically setting the persistence threshold parameter that influences the accurate bracketing of the roots.