Approximating Continuous Functions on Persistence Diagrams Using Template Functions

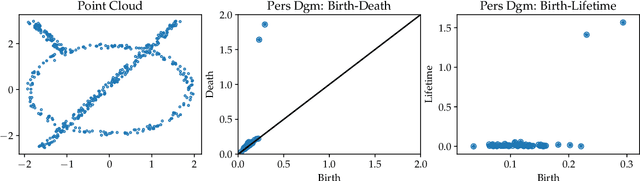
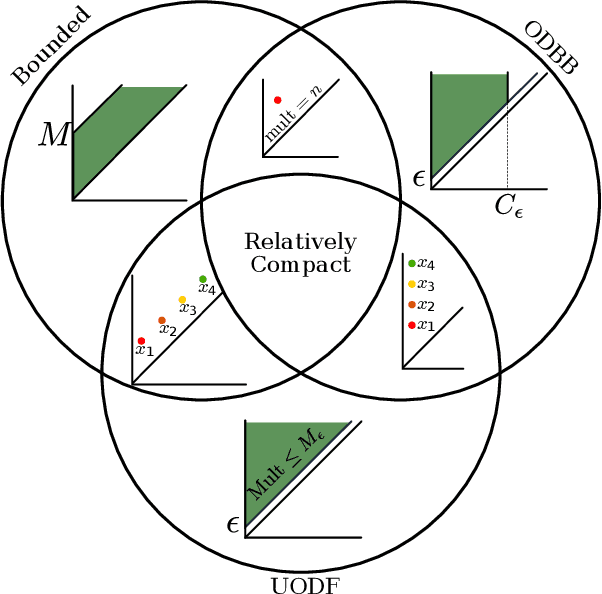
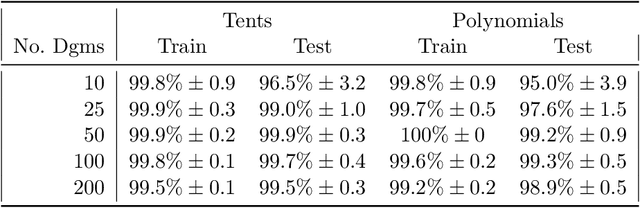
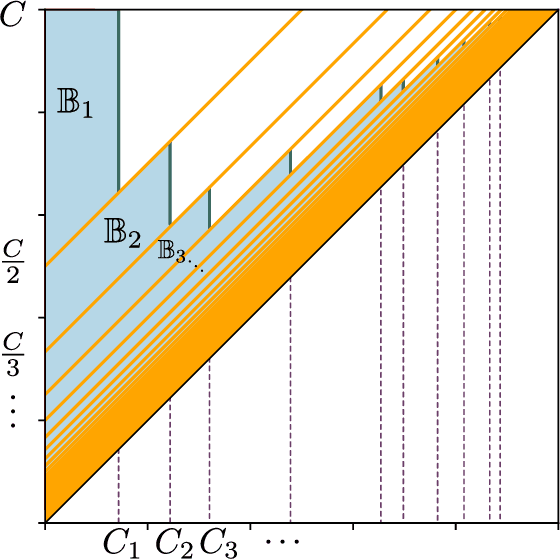
The persistence diagram is an increasingly useful tool from Topological Data Analysis, but its use alongside typical machine learning techniques requires mathematical finesse. The most success to date has come from methods that map persistence diagrams into $\mathbb{R}^n$, in a way which maximizes the structure preserved. This process is commonly referred to as featurization. In this paper, we describe a mathematical framework for featurization using template functions. These functions are general as they are only required to be continuous and compactly supported. We discuss two realizations: tent functions, which emphasize the local contributions of points in a persistence diagram, and interpolating polynomials, which capture global pairwise interactions. We combine the resulting features with classification and regression algorithms on several examples including shape data and the Rossler system. Our results show that using template functions yields high accuracy rates that match and often exceed those of existing featurization methods. One counter-intuitive observation is that in most cases using interpolating polynomials, where each point contributes globally to the feature vector, yields significantly better results than using tent functions, where the contribution of each point is localized. Along the way, we provide a complete characterization of compactness in the space of persistence diagrams.