TopoX: A Suite of Python Packages for Machine Learning on Topological Domains

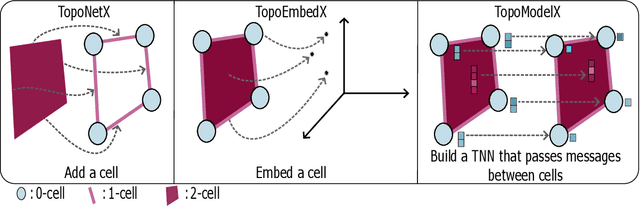
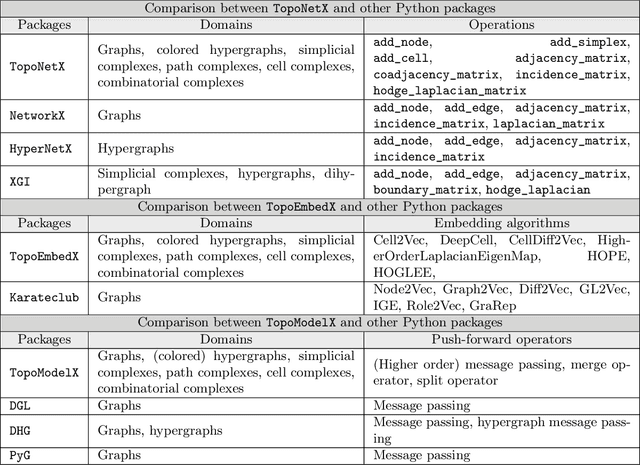
We introduce topox, a Python software suite that provides reliable and user-friendly building blocks for computing and machine learning on topological domains that extend graphs: hypergraphs, simplicial, cellular, path and combinatorial complexes. topox consists of three packages: toponetx facilitates constructing and computing on these domains, including working with nodes, edges and higher-order cells; topoembedx provides methods to embed topological domains into vector spaces, akin to popular graph-based embedding algorithms such as node2vec; topomodelx is built on top of PyTorch and offers a comprehensive toolbox of higher-order message passing functions for neural networks on topological domains. The extensively documented and unit-tested source code of topox is available under MIT license at https://github.com/pyt-team.

ICML 2023 Topological Deep Learning Challenge : Design and Results

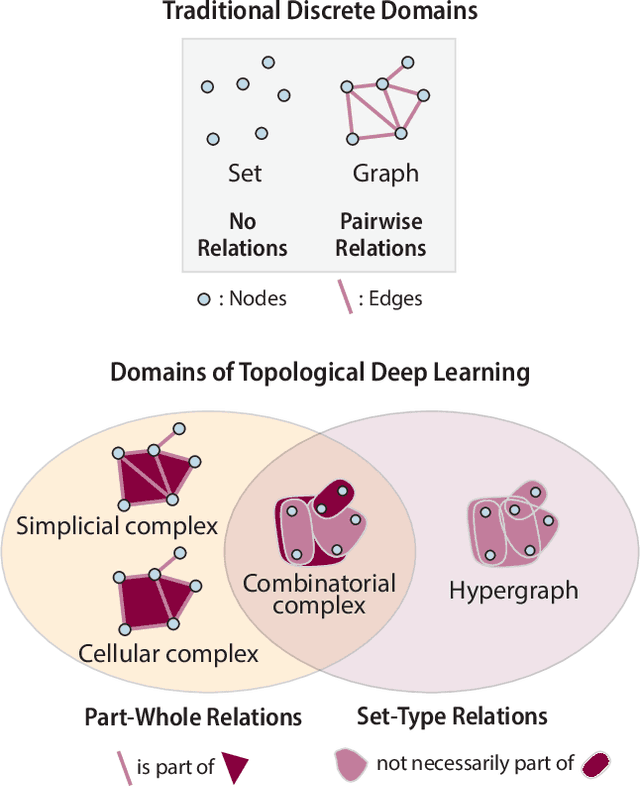
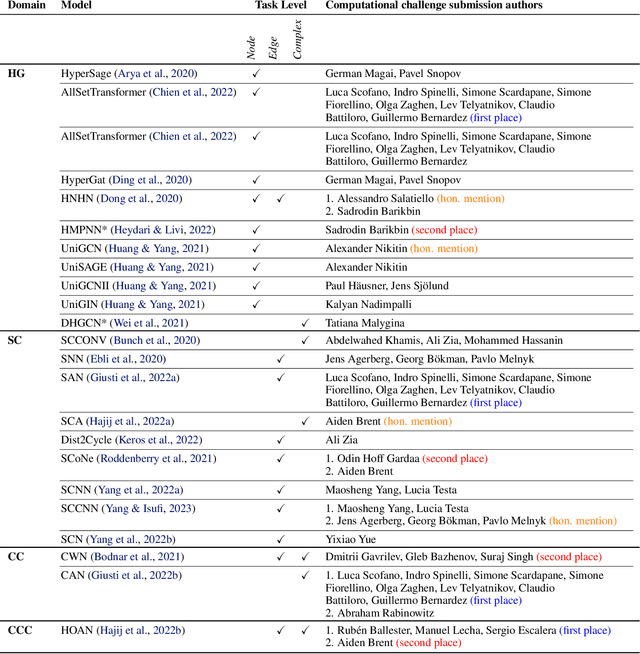
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

CLAMS: A Cluster Ambiguity Measure for Estimating Perceptual Variability in Visual Clustering

Visual clustering is a common perceptual task in scatterplots that supports diverse analytics tasks (e.g., cluster identification). However, even with the same scatterplot, the ways of perceiving clusters (i.e., conducting visual clustering) can differ due to the differences among individuals and ambiguous cluster boundaries. Although such perceptual variability casts doubt on the reliability of data analysis based on visual clustering, we lack a systematic way to efficiently assess this variability. In this research, we study perceptual variability in conducting visual clustering, which we call Cluster Ambiguity. To this end, we introduce CLAMS, a data-driven visual quality measure for automatically predicting cluster ambiguity in monochrome scatterplots. We first conduct a qualitative study to identify key factors that affect the visual separation of clusters (e.g., proximity or size difference between clusters). Based on study findings, we deploy a regression module that estimates the human-judged separability of two clusters. Then, CLAMS predicts cluster ambiguity by analyzing the aggregated results of all pairwise separability between clusters that are generated by the module. CLAMS outperforms widely-used clustering techniques in predicting ground truth cluster ambiguity. Meanwhile, CLAMS exhibits performance on par with human annotators. We conclude our work by presenting two applications for optimizing and benchmarking data mining techniques using CLAMS. The interactive demo of CLAMS is available at clusterambiguity.dev.

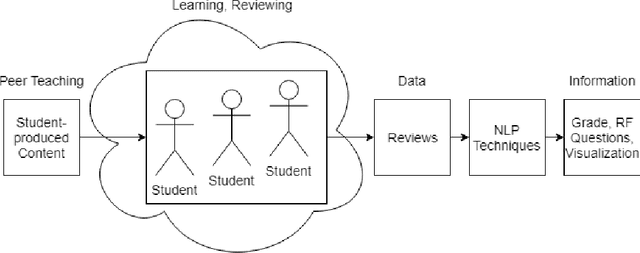
Polarity in the Classroom: A Case Study Leveraging Peer Sentiment Toward Scalable Assessment

Accurately grading open-ended assignments in large or massive open online courses (MOOCs) is non-trivial. Peer review is a promising solution but can be unreliable due to few reviewers and an unevaluated review form. To date, no work has 1) leveraged sentiment analysis in the peer-review process to inform or validate grades or 2) utilized aspect extraction to craft a review form from what students actually communicated. Our work utilizes, rather than discards, student data from review form comments to deliver better information to the instructor. In this work, we detail the process by which we create our domain-dependent lexicon and aspect-informed review form as well as our entire sentiment analysis algorithm which provides a fine-grained sentiment score from text alone. We end by analyzing validity and discussing conclusions from our corpus of over 6800 peer reviews from nine courses to understand the viability of sentiment in the classroom for increasing the information from and reliability of grading open-ended assignments in large courses.

Graph Similarity Using PageRank and Persistent Homology

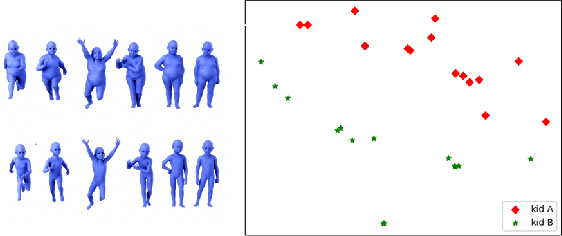
The PageRank of a graph is a scalar function defined on the node set of the graph which encodes nodes centrality information of the graph. In this work, we utilize the PageRank function on the lower-star filtration of the graph as input to persistent homology to study the problem of graph similarity. By representing each graph as a persistence diagram, we can then compare outputs using the bottleneck distance. We show the effectiveness of our method by utilizing it on two shape mesh datasets.

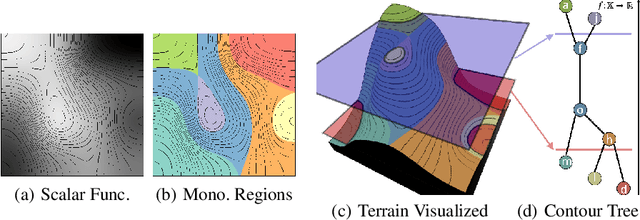
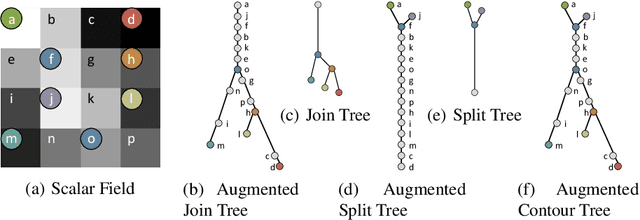
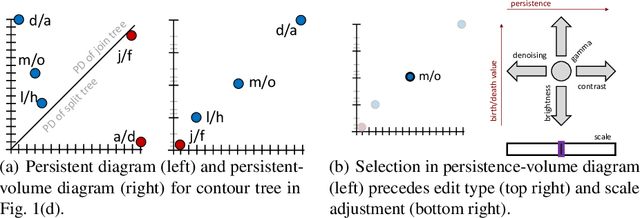
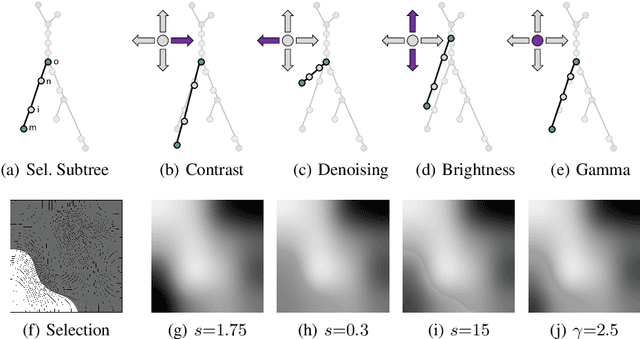
Topologically-Guided Color Image Enhancement

Enhancement is an important step in post-processing digital images for personal use, in medical imaging, and for object recognition. Most existing manual techniques rely on region selection, similarity, and/or thresholding for editing, never really considering the topological structure of the image. In this paper, we leverage the contour tree to extract a hierarchical representation of the topology of an image. We propose 4 topology-aware transfer functions for editing features of the image using local topological properties, instead of global image properties. Finally, we evaluate our approach with grayscale and color images.

Mesh Learning Using Persistent Homology on the Laplacian Eigenfunctions

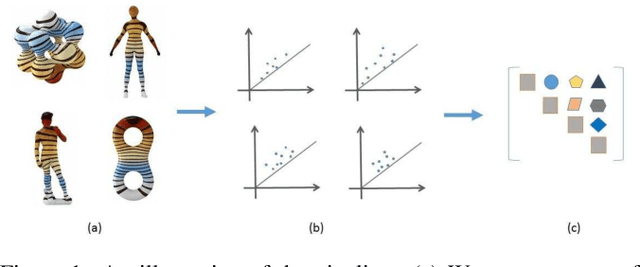
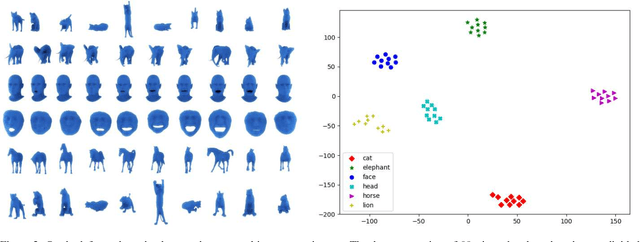
We use persistent homology along with the eigenfunctions of the Laplacian to study similarity amongst triangulated 2-manifolds. Our method relies on studying the lower-star filtration induced by the eigenfunctions of the Laplacian. This gives us a shape descriptor that inherits the rich information encoded in the eigenfunctions of the Laplacian. Moreover, the similarity between these descriptors can be easily computed using tools that are readily available in Topological Data Analysis. We provide experiments to illustrate the effectiveness of the proposed method.

An Efficient Data Retrieval Parallel Reeb Graph Algorithm

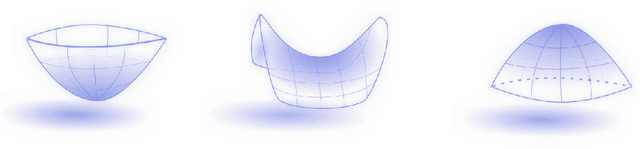
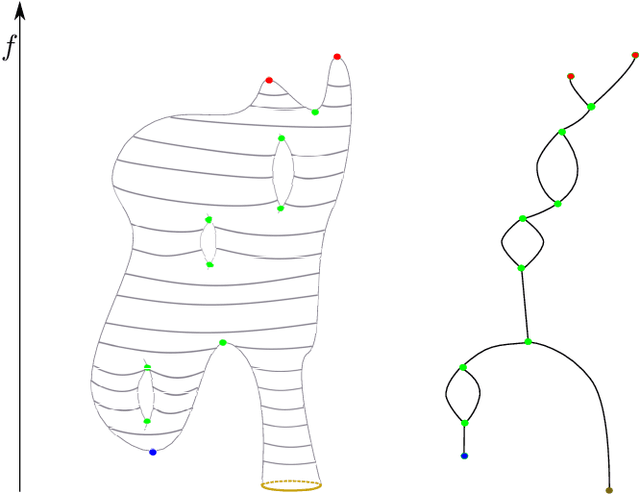
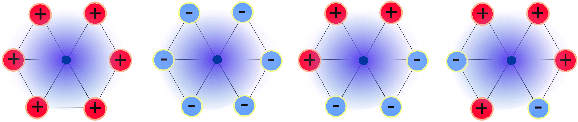
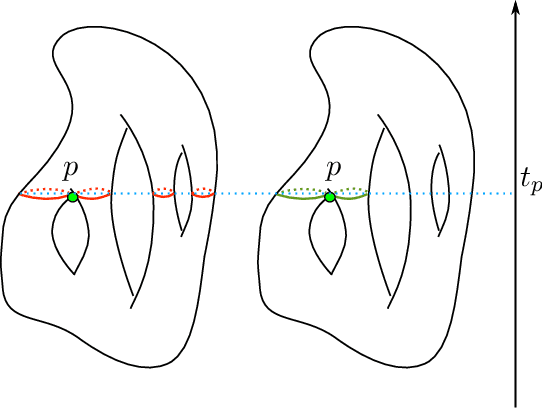
The Reeb graph of a scalar function defined on a domain gives a topological meaningful summary of that domain. Reeb graphs have been shown in the past decade to be of great importance in geometric processing, image processing, computer graphics and computational topology. The demand to compute large data sets has increased in the last decade and hence the consideration of parallelization of topological computations. We propose a parallel Reeb graph algorithm on triangulated meshes with and without a boundary. Furthermore, we give a description for extracting the original manifold data from the Reeb graph structure. As an application, we show how our algorithm can be utilized in mesh segmentation algorithms.