An Efficient Data Retrieval Parallel Reeb Graph Algorithm

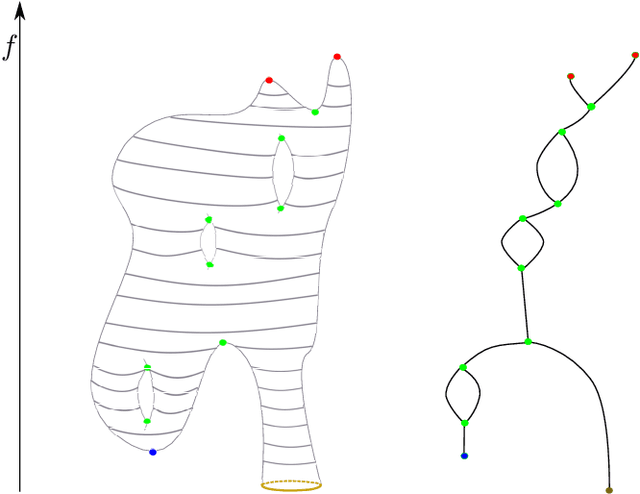
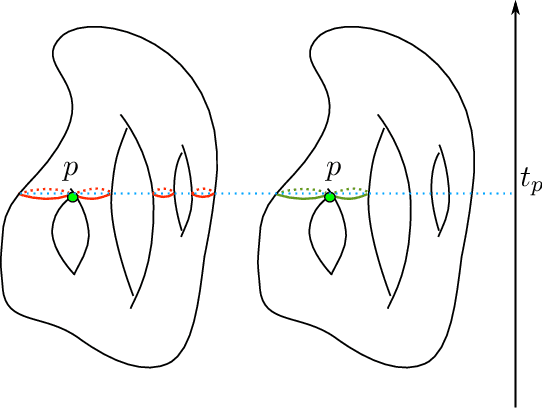
The Reeb graph of a scalar function defined on a domain gives a topological meaningful summary of that domain. Reeb graphs have been shown in the past decade to be of great importance in geometric processing, image processing, computer graphics and computational topology. The demand to compute large data sets has increased in the last decade and hence the consideration of parallelization of topological computations. We propose a parallel Reeb graph algorithm on triangulated meshes with and without a boundary. Furthermore, we give a description for extracting the original manifold data from the Reeb graph structure. As an application, we show how our algorithm can be utilized in mesh segmentation algorithms.