A Pipeline for Data-Driven Learning of Topological Features with Applications to Protein Stability Prediction

In this paper, we propose a data-driven method to learn interpretable topological features of biomolecular data and demonstrate the efficacy of parsimonious models trained on topological features in predicting the stability of synthetic mini proteins. We compare models that leverage automatically-learned structural features against models trained on a large set of biophysical features determined by subject-matter experts (SME). Our models, based only on topological features of the protein structures, achieved 92%-99% of the performance of SME-based models in terms of the average precision score. By interrogating model performance and feature importance metrics, we extract numerous insights that uncover high correlations between topological features and SME features. We further showcase how combining topological features and SME features can lead to improved model performance over either feature set used in isolation, suggesting that, in some settings, topological features may provide new discriminating information not captured in existing SME features that are useful for protein stability prediction.

Persistence Images: A Stable Vector Representation of Persistent Homology

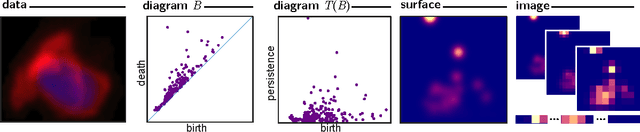
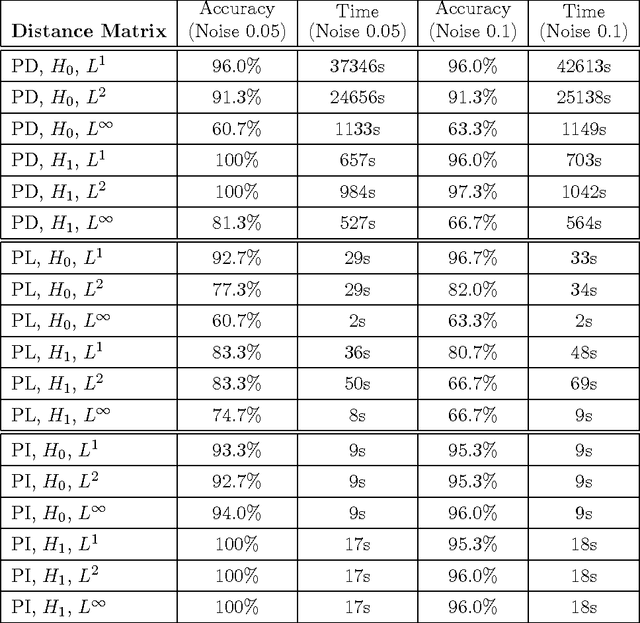
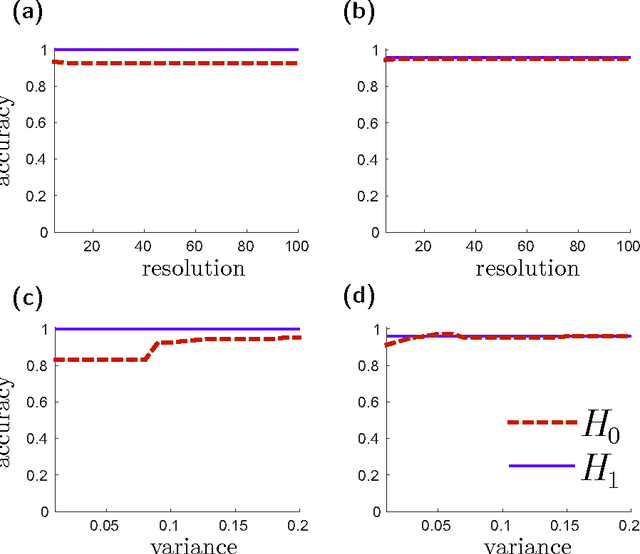
Many datasets can be viewed as a noisy sampling of an underlying space, and tools from topological data analysis can characterize this structure for the purpose of knowledge discovery. One such tool is persistent homology, which provides a multiscale description of the homological features within a dataset. A useful representation of this homological information is a persistence diagram (PD). Efforts have been made to map PDs into spaces with additional structure valuable to machine learning tasks. We convert a PD to a finite-dimensional vector representation which we call a persistence image (PI), and prove the stability of this transformation with respect to small perturbations in the inputs. The discriminatory power of PIs is compared against existing methods, showing significant performance gains. We explore the use of PIs with vector-based machine learning tools, such as linear sparse support vector machines, which identify features containing discriminating topological information. Finally, high accuracy inference of parameter values from the dynamic output of a discrete dynamical system (the linked twist map) and a partial differential equation (the anisotropic Kuramoto-Sivashinsky equation) provide a novel application of the discriminatory power of PIs.