Amish Mishra
MONSTER: Monash Scalable Time Series Evaluation Repository
Feb 21, 2025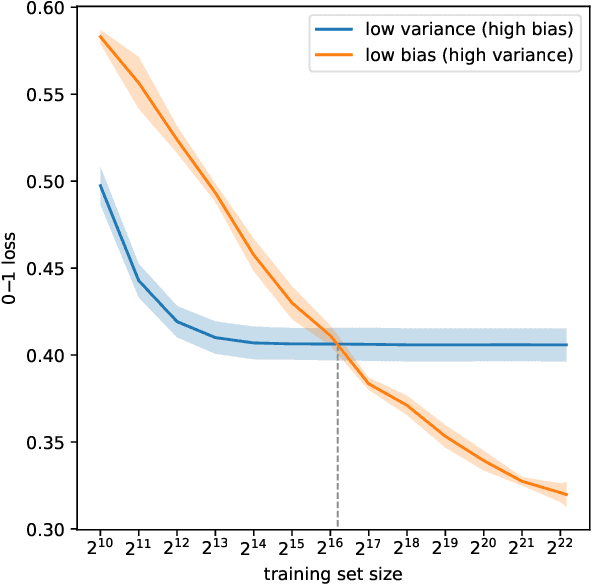
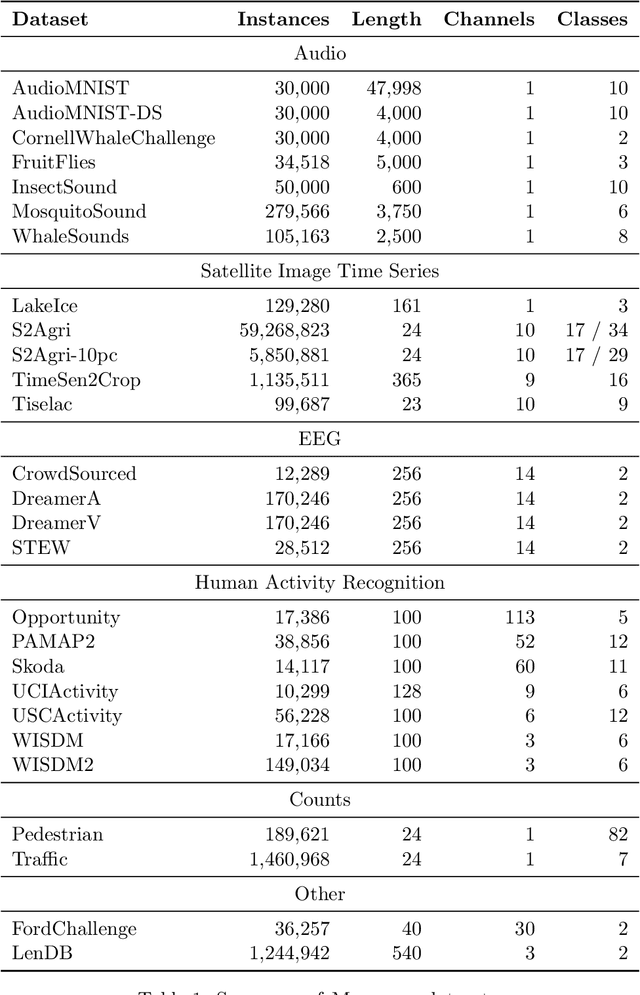
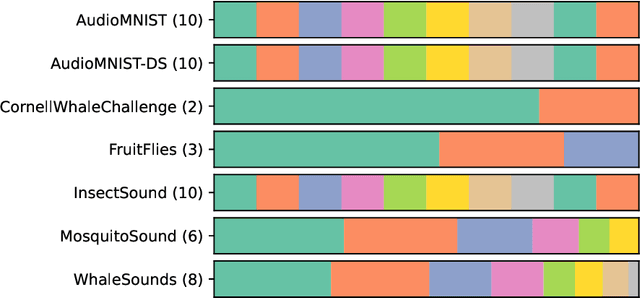
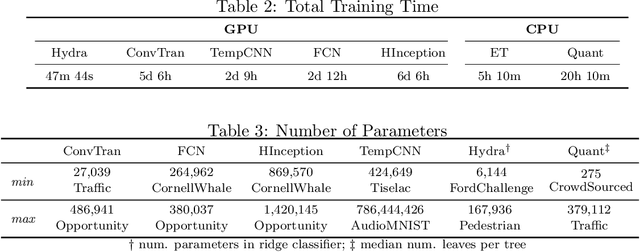
Abstract:We introduce MONSTER-the MONash Scalable Time Series Evaluation Repository-a collection of large datasets for time series classification. The field of time series classification has benefitted from common benchmarks set by the UCR and UEA time series classification repositories. However, the datasets in these benchmarks are small, with median sizes of 217 and 255 examples, respectively. In consequence they favour a narrow subspace of models that are optimised to achieve low classification error on a wide variety of smaller datasets, that is, models that minimise variance, and give little weight to computational issues such as scalability. Our hope is to diversify the field by introducing benchmarks using larger datasets. We believe that there is enormous potential for new progress in the field by engaging with the theoretical and practical challenges of learning effectively from larger quantities of data.
A Pipeline for Data-Driven Learning of Topological Features with Applications to Protein Stability Prediction
Aug 09, 2024Abstract:In this paper, we propose a data-driven method to learn interpretable topological features of biomolecular data and demonstrate the efficacy of parsimonious models trained on topological features in predicting the stability of synthetic mini proteins. We compare models that leverage automatically-learned structural features against models trained on a large set of biophysical features determined by subject-matter experts (SME). Our models, based only on topological features of the protein structures, achieved 92%-99% of the performance of SME-based models in terms of the average precision score. By interrogating model performance and feature importance metrics, we extract numerous insights that uncover high correlations between topological features and SME features. We further showcase how combining topological features and SME features can lead to improved model performance over either feature set used in isolation, suggesting that, in some settings, topological features may provide new discriminating information not captured in existing SME features that are useful for protein stability prediction.
Stability and Machine Learning Applications of Persistent Homology Using the Delaunay-Rips Complex
Mar 02, 2023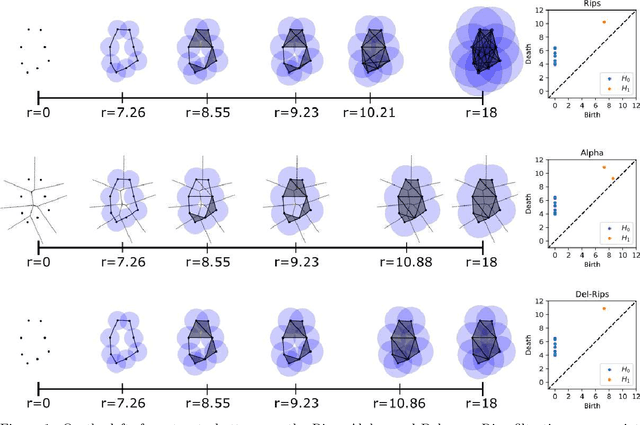
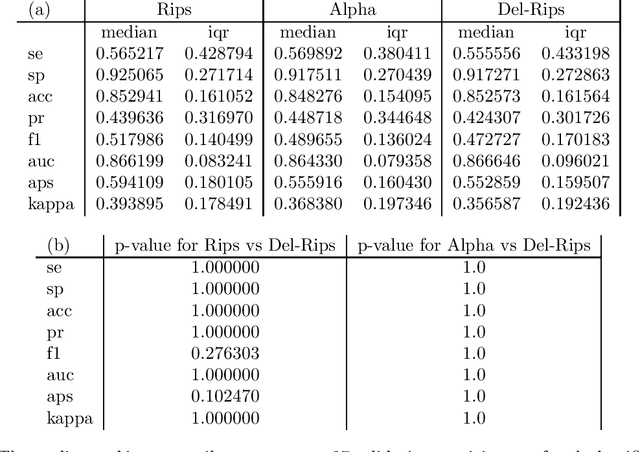
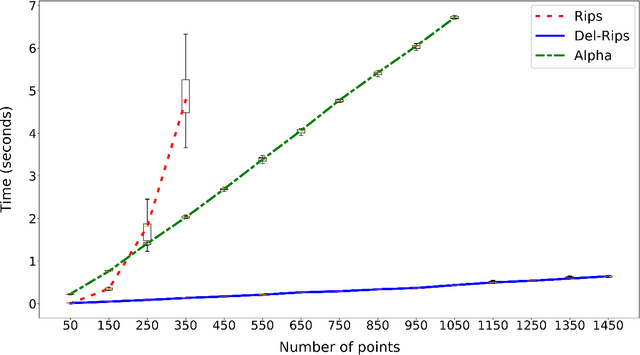
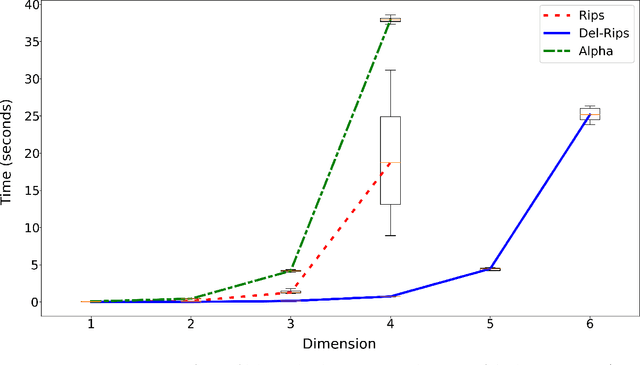
Abstract:In this paper we define, implement, and investigate a simplicial complex construction for computing persistent homology of Euclidean point cloud data, which we call the Delaunay-Rips complex (DR). Assigning the Vietoris-Rips weights to simplices, DR experiences speed-up in the persistence calculations by only considering simplices that appear in the Delaunay triangulation of the point cloud. We document and compare a Python implementation of DR with other simplicial complex constructions for generating persistence diagrams. By imposing sufficient conditions on point cloud data, we are able to theoretically justify the stability of the persistence diagrams produced using DR. When the Delaunay triangulation of the point cloud changes under perturbations of the points, we prove that DR-produced persistence diagrams exhibit instability. Since we cannot guarantee that real-world data will satisfy our stability conditions, we demonstrate the practical robustness of DR for persistent homology in comparison with other simplicial complexes in machine learning applications. We find in our experiments that using DR for an ML-TDA pipeline performs comparatively well as using other simplicial complex constructions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge