(Quasi)Periodicity Quantification in Video Data, Using Topology
Paper and Code
Jan 21, 2018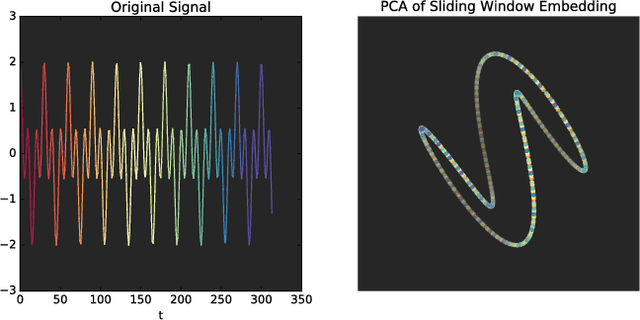
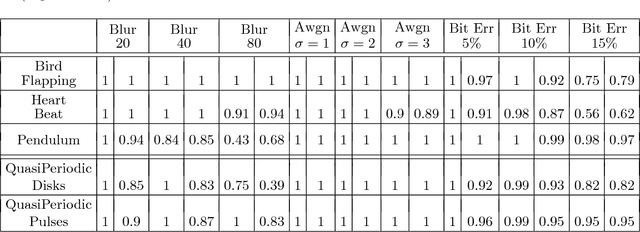

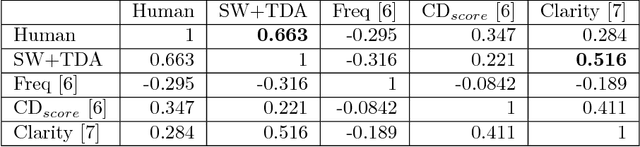
This work introduces a novel framework for quantifying the presence and strength of recurrent dynamics in video data. Specifically, we provide continuous measures of periodicity (perfect repetition) and quasiperiodicity (superposition of periodic modes with non-commensurate periods), in a way which does not require segmentation, training, object tracking or 1-dimensional surrogate signals. Our methodology operates directly on video data. The approach combines ideas from nonlinear time series analysis (delay embeddings) and computational topology (persistent homology), by translating the problem of finding recurrent dynamics in video data, into the problem of determining the circularity or toroidality of an associated geometric space. Through extensive testing, we show the robustness of our scores with respect to several noise models/levels, we show that our periodicity score is superior to other methods when compared to human-generated periodicity rankings, and furthermore, we show that our quasiperiodicity score clearly indicates the presence of biphonation in videos of vibrating vocal folds, which has never before been accomplished end to end quantitatively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge