Quiver Laplacians and Feature Selection

The challenge of selecting the most relevant features of a given dataset arises ubiquitously in data analysis and dimensionality reduction. However, features found to be of high importance for the entire dataset may not be relevant to subsets of interest, and vice versa. Given a feature selector and a fixed decomposition of the data into subsets, we describe a method for identifying selected features which are compatible with the decomposition into subsets. We achieve this by re-framing the problem of finding compatible features to one of finding sections of a suitable quiver representation. In order to approximate such sections, we then introduce a Laplacian operator for quiver representations valued in Hilbert spaces. We provide explicit bounds on how the spectrum of a quiver Laplacian changes when the representation and the underlying quiver are modified in certain natural ways. Finally, we apply this machinery to the study of peak-calling algorithms which measure chromatin accessibility in single-cell data. We demonstrate that eigenvectors of the associated quiver Laplacian yield locally and globally compatible features.

Topological fingerprints for audio identification

We present a topological audio fingerprinting approach for robustly identifying duplicate audio tracks. Our method applies persistent homology on local spectral decompositions of audio signals, using filtered cubical complexes computed from mel-spectrograms. By encoding the audio content in terms of local Betti curves, our topological audio fingerprints enable accurate detection of time-aligned audio matchings. Experimental results demonstrate the accuracy of our algorithm in the detection of tracks with the same audio content, even when subjected to various obfuscations. Our approach outperforms existing methods in scenarios involving topological distortions, such as time stretching and pitch shifting.

Multiscale methods for signal selection in single-cell data

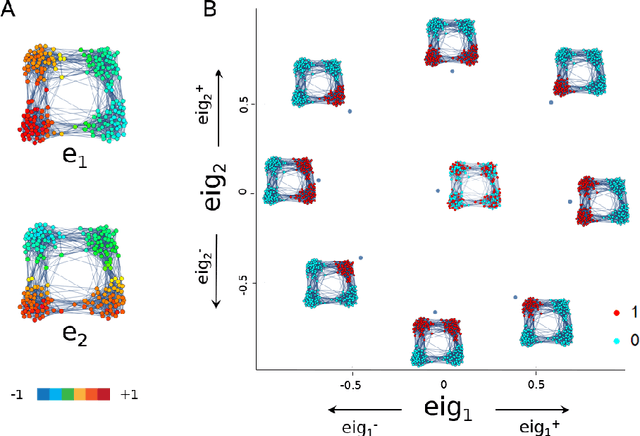
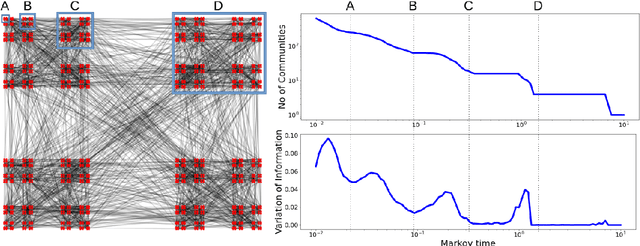
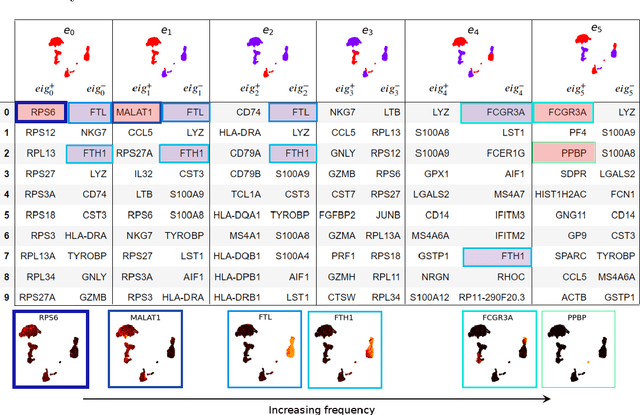
Analysis of single-cell transcriptomics often relies on clustering cells and then performing differential gene expression (DGE) to identify genes that vary between these clusters. These discrete analyses successfully determine cell types and markers; however, continuous variation within and between cell types may not be detected. We propose three topologically-motivated mathematical methods for unsupervised feature selection that consider discrete and continuous transcriptional patterns on an equal footing across multiple scales simultaneously. Eigenscores ($\mathrm{eig}_i$) rank signals or genes based on their correspondence to low-frequency intrinsic patterning in the data using the spectral decomposition of the graph Laplacian. The multiscale Laplacian score (MLS) is an unsupervised method for locating relevant scales in data and selecting the genes that are coherently expressed at these respective scales. The persistent Rayleigh quotient (PRQ) takes data equipped with a filtration, allowing separation of genes with different roles in a bifurcation process (e.g. pseudo-time). We demonstrate the utility of these techniques by applying them to published single-cell transcriptomics data sets. The methods validate previously identified genes and detect additional genes with coherent expression patterns. By studying the interaction between gene signals and the geometry of the underlying space, the three methods give multidimensional rankings of the genes and visualisation of relationships between them.

Tensor clustering with algebraic constraints gives interpretable groups of crosstalk mechanisms in breast cancer

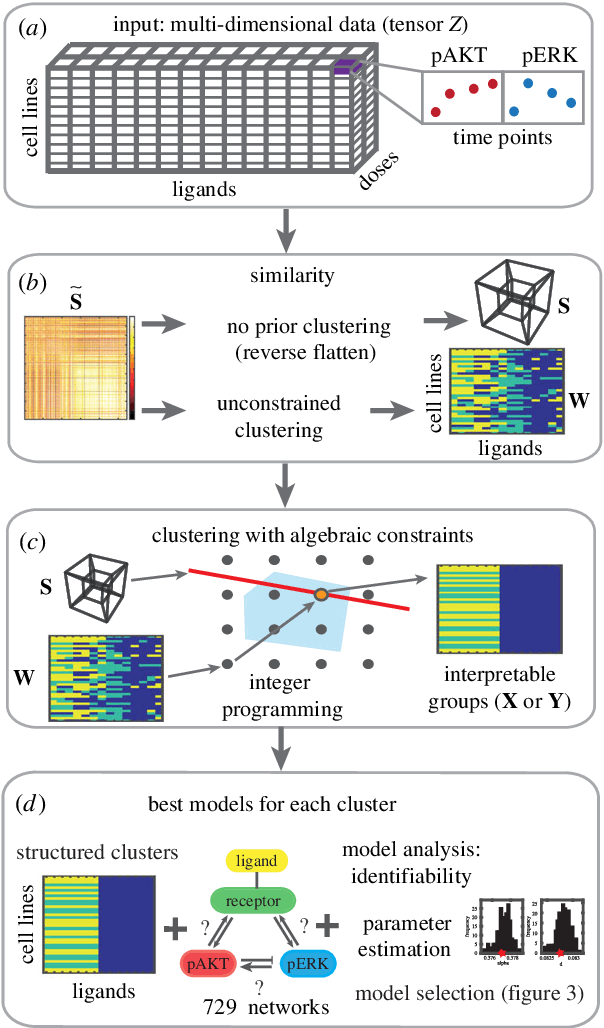
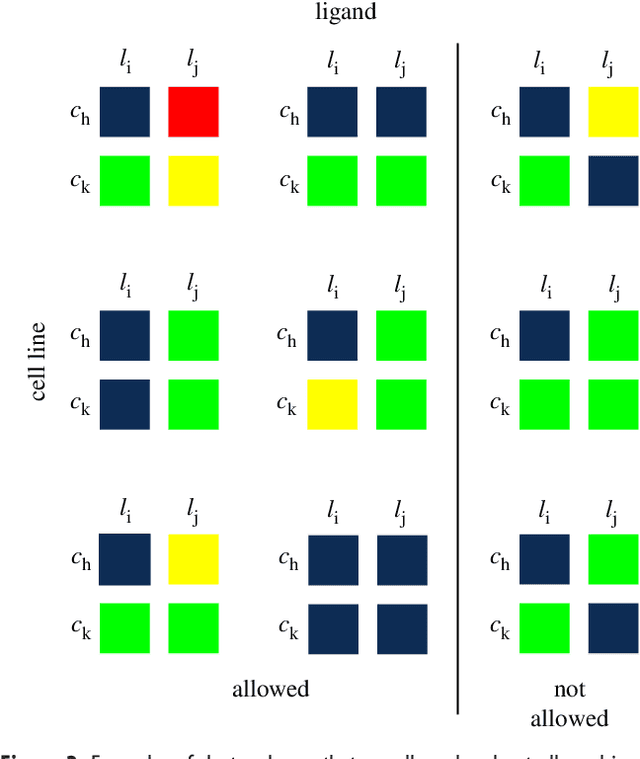
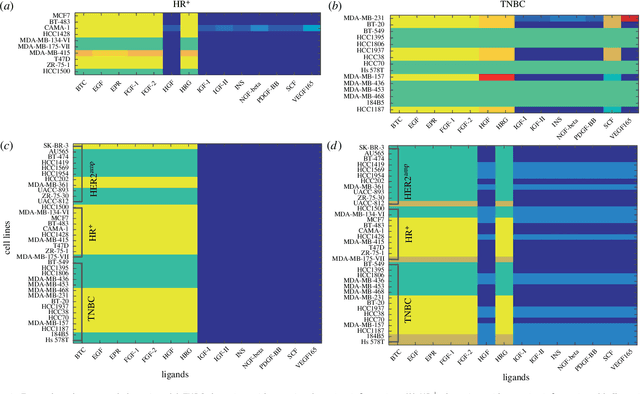
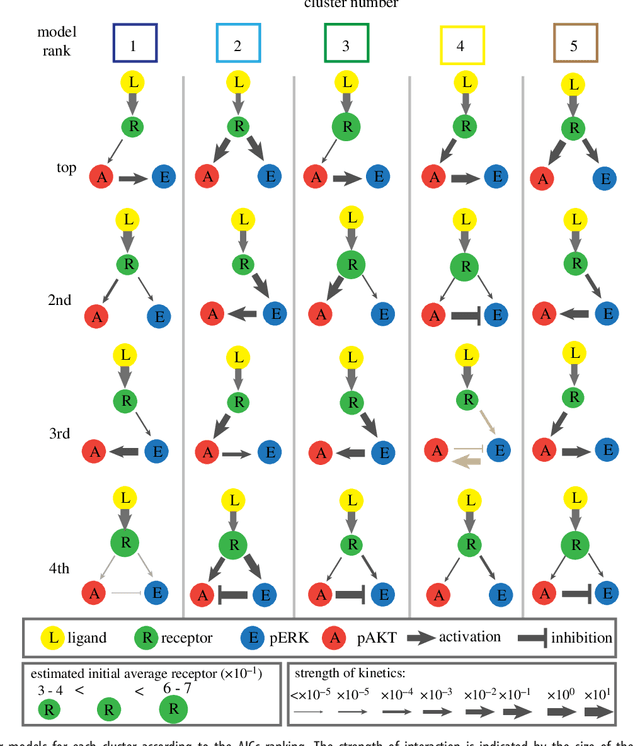
We introduce a tensor-based clustering method to extract sparse, low-dimensional structure from high-dimensional, multi-indexed datasets. Specifically, this framework is designed to enable detection of clusters of data in the presence of structural requirements which we encode as algebraic constraints in a linear program. We illustrate our method on a collection of experiments measuring the response of genetically diverse breast cancer cell lines to an array of ligands. Each experiment consists of a cell line-ligand combination, and contains time-course measurements of the early-signalling kinases MAPK and AKT at two different ligand dose levels. By imposing appropriate structural constraints and respecting the multi-indexed structure of the data, our clustering analysis can be optimized for biological interpretation and therapeutic understanding. We then perform a systematic, large-scale exploration of mechanistic models of MAPK-AKT crosstalk for each cluster. This analysis allows us to quantify the heterogeneity of breast cancer cell subtypes, and leads to hypotheses about the mechanisms by which cell lines respond to ligands. Our clustering method is general and can be tailored to a variety of applications in science and industry.