Quiver Laplacians and Feature Selection

The challenge of selecting the most relevant features of a given dataset arises ubiquitously in data analysis and dimensionality reduction. However, features found to be of high importance for the entire dataset may not be relevant to subsets of interest, and vice versa. Given a feature selector and a fixed decomposition of the data into subsets, we describe a method for identifying selected features which are compatible with the decomposition into subsets. We achieve this by re-framing the problem of finding compatible features to one of finding sections of a suitable quiver representation. In order to approximate such sections, we then introduce a Laplacian operator for quiver representations valued in Hilbert spaces. We provide explicit bounds on how the spectrum of a quiver Laplacian changes when the representation and the underlying quiver are modified in certain natural ways. Finally, we apply this machinery to the study of peak-calling algorithms which measure chromatin accessibility in single-cell data. We demonstrate that eigenvectors of the associated quiver Laplacian yield locally and globally compatible features.

HADES: Fast Singularity Detection with Local Measure Comparison

We introduce Hades, an unsupervised algorithm to detect singularities in data. This algorithm employs a kernel goodness-of-fit test, and as a consequence it is much faster and far more scaleable than the existing topology-based alternatives. Using tools from differential geometry and optimal transport theory, we prove that Hades correctly detects singularities with high probability when the data sample lives on a transverse intersection of equidimensional manifolds. In computational experiments, Hades recovers singularities in synthetically generated data, branching points in road network data, intersection rings in molecular conformation space, and anomalies in image data.

Dist2Cycle: A Simplicial Neural Network for Homology Localization

Simplicial complexes can be viewed as high dimensional generalizations of graphs that explicitly encode multi-way ordered relations between vertices at different resolutions, all at once. This concept is central towards detection of higher dimensional topological features of data, features to which graphs, encoding only pairwise relationships, remain oblivious. While attempts have been made to extend Graph Neural Networks (GNNs) to a simplicial complex setting, the methods do not inherently exploit, or reason about, the underlying topological structure of the network. We propose a graph convolutional model for learning functions parametrized by the $k$-homological features of simplicial complexes. By spectrally manipulating their combinatorial $k$-dimensional Hodge Laplacians, the proposed model enables learning topological features of the underlying simplicial complexes, specifically, the distance of each $k$-simplex from the nearest "optimal" $k$-th homology generator, effectively providing an alternative to homology localization.

Tangent Space and Dimension Estimation with the Wasserstein Distance

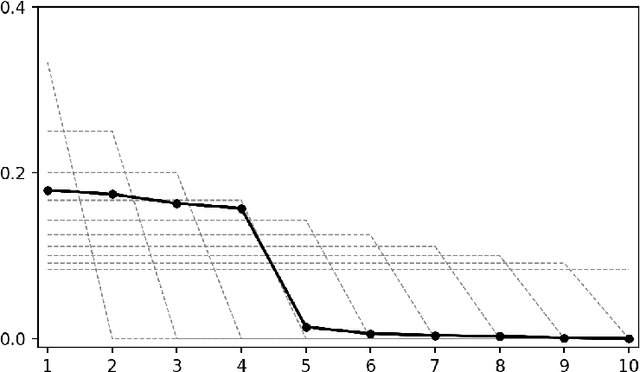
We provide explicit bounds on the number of sample points required to estimate tangent spaces and intrinsic dimensions of (smooth, compact) Euclidean submanifolds via local principal component analysis. Our approach directly estimates covariance matrices locally, which simultaneously allows estimating both the tangent spaces and the intrinsic dimension of a manifold. The key arguments involve a matrix concentration inequality, a Wasserstein bound for flattening a manifold, and a Lipschitz relation for the covariance matrix with respect to the Wasserstein distance.

Persistence paths and signature features in topological data analysis

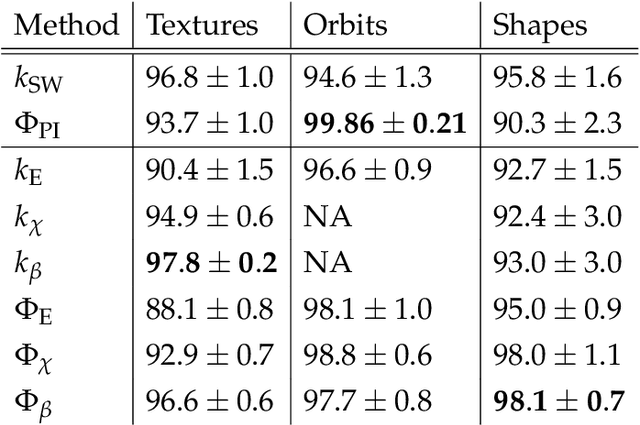
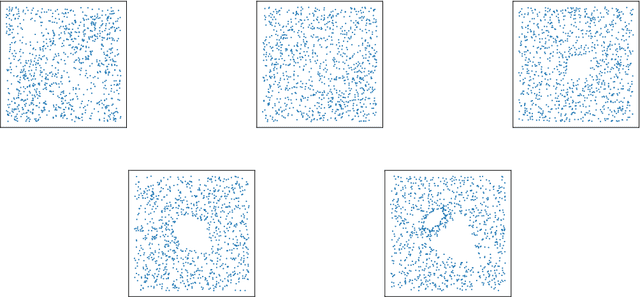
We introduce a new feature map for barcodes that arise in persistent homology computation. The main idea is to first realize each barcode as a path in a convenient vector space, and to then compute its path signature which takes values in the tensor algebra of that vector space. The composition of these two operations - barcode to path, path to tensor series - results in a feature map that has several desirable properties for statistical learning, such as universality and characteristicness, and achieves state-of-the-art results on common classification benchmarks.