Feature Engineering with Regularity Structures

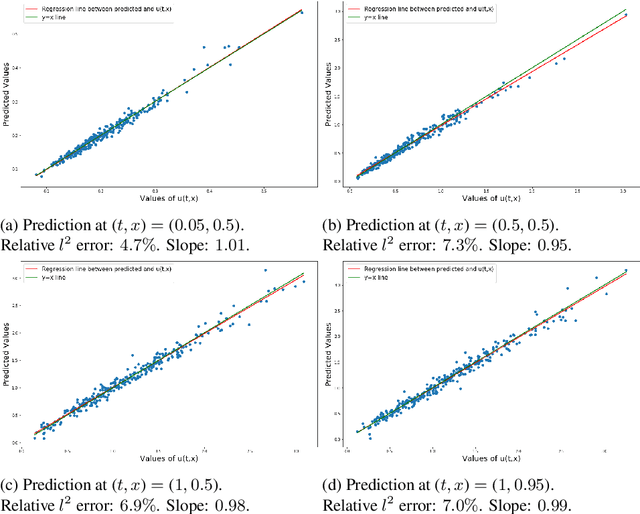
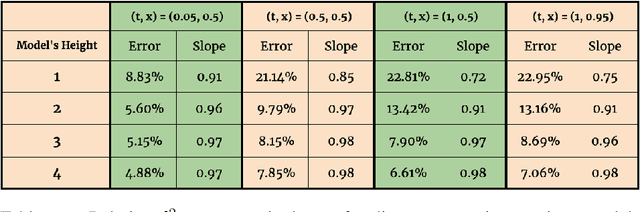
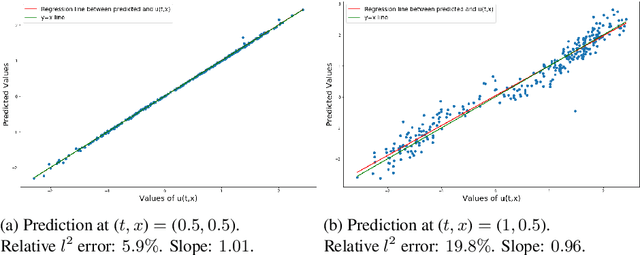
We investigate the use of models from the theory of regularity structure as features in machine learning tasks. A model is a multi-linear function of a space-time signal designed to well-approximate solutions to partial differential equations (PDEs), even in low regularity regimes. Models can be seen as natural multi-dimensional generalisations of signatures of paths; our work therefore aims to extend the recent use of signatures in data science beyond the context of time-ordered data. We provide a flexible definition of a model feature vector associated to a space-time signal, along with two algorithms which illustrate ways in which these features can be combined with linear regression. We apply these algorithms in several numerical experiments designed to learn solutions to PDEs with a given forcing and boundary data. Our experiments include semi-linear parabolic and wave equations with forcing, and Burgers' equation with no forcing. We find an advantage in favour of our algorithms when compared to several alternative methods. Additionally, in the experiment with Burgers' equation, we noticed stability in the prediction power when noise is added to the observations.

Signature moments to characterize laws of stochastic processes

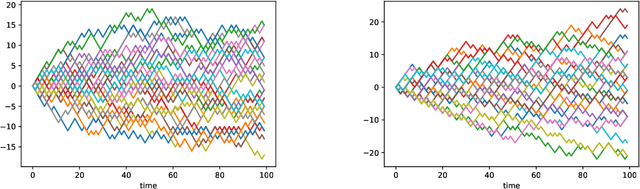
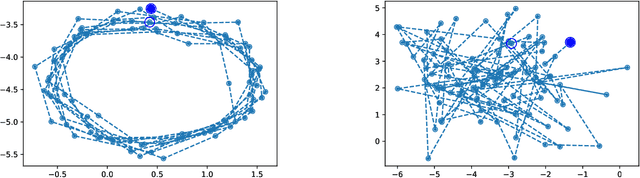
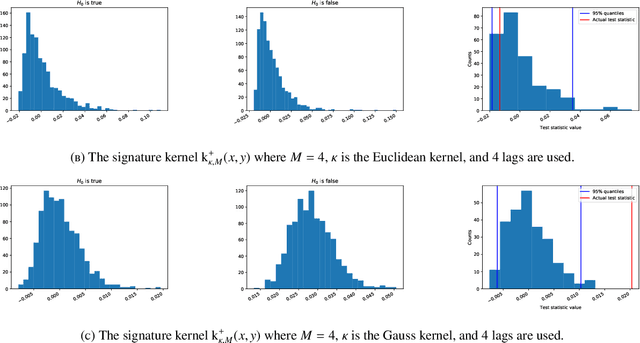
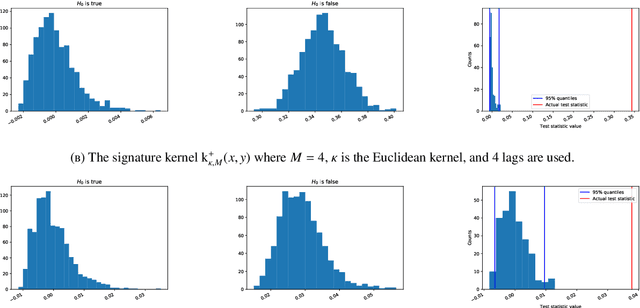
The normalized sequence of moments characterizes the law of any finite-dimensional random variable. We prove an analogous result for path-valued random variables, that is stochastic processes, by using the normalized sequence of signature moments. We use this to define a metric for laws of stochastic processes. This metric can be efficiently estimated from finite samples, even if the stochastic processes themselves evolve in high-dimensional state spaces. As an application, we provide a non-parametric two-sample hypothesis test for laws of stochastic processes.

Persistence paths and signature features in topological data analysis

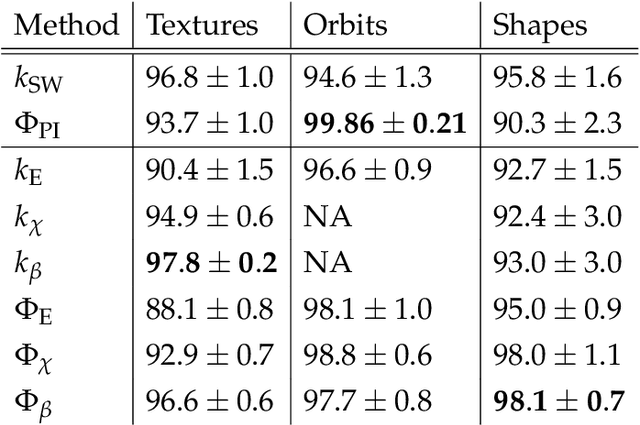
We introduce a new feature map for barcodes that arise in persistent homology computation. The main idea is to first realize each barcode as a path in a convenient vector space, and to then compute its path signature which takes values in the tensor algebra of that vector space. The composition of these two operations - barcode to path, path to tensor series - results in a feature map that has several desirable properties for statistical learning, such as universality and characteristicness, and achieves state-of-the-art results on common classification benchmarks.

A Primer on the Signature Method in Machine Learning

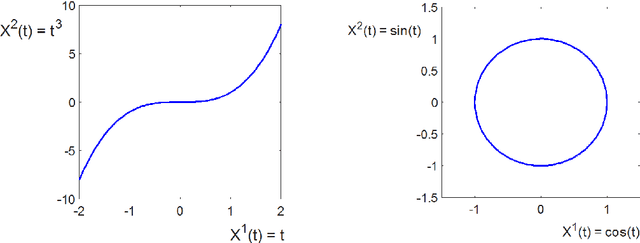
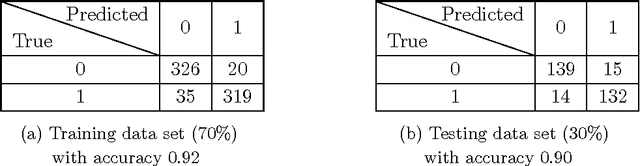
In these notes, we wish to provide an introduction to the signature method, focusing on its basic theoretical properties and recent numerical applications. The notes are split into two parts. The first part focuses on the definition and fundamental properties of the signature of a path, or the path signature. We have aimed for a minimalistic approach, assuming only familiarity with classical real analysis and integration theory, and supplementing theory with straightforward examples. We have chosen to focus in detail on the principle properties of the signature which we believe are fundamental to understanding its role in applications. We also present an informal discussion on some of its deeper properties and briefly mention the role of the signature in rough paths theory, which we hope could serve as a light introduction to rough paths for the interested reader. The second part of these notes discusses practical applications of the path signature to the area of machine learning. The signature approach represents a non-parametric way for extraction of characteristic features from data. The data are converted into a multi-dimensional path by means of various embedding algorithms and then processed for computation of individual terms of the signature which summarise certain information contained in the data. The signature thus transforms raw data into a set of features which are used in machine learning tasks. We will review current progress in applications of signatures to machine learning problems.