A Primer on the Signature Method in Machine Learning
Paper and Code
Mar 11, 2016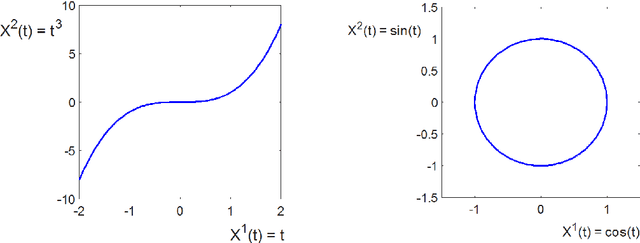
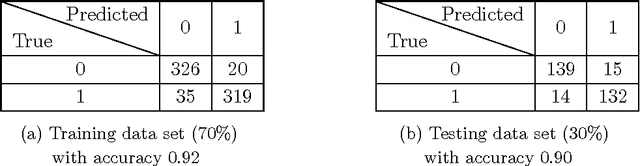
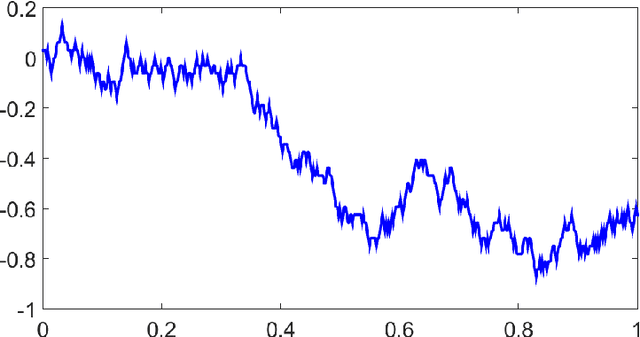
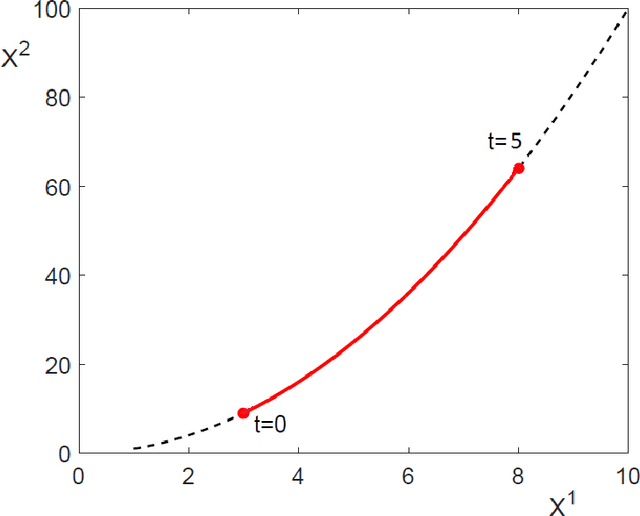
In these notes, we wish to provide an introduction to the signature method, focusing on its basic theoretical properties and recent numerical applications. The notes are split into two parts. The first part focuses on the definition and fundamental properties of the signature of a path, or the path signature. We have aimed for a minimalistic approach, assuming only familiarity with classical real analysis and integration theory, and supplementing theory with straightforward examples. We have chosen to focus in detail on the principle properties of the signature which we believe are fundamental to understanding its role in applications. We also present an informal discussion on some of its deeper properties and briefly mention the role of the signature in rough paths theory, which we hope could serve as a light introduction to rough paths for the interested reader. The second part of these notes discusses practical applications of the path signature to the area of machine learning. The signature approach represents a non-parametric way for extraction of characteristic features from data. The data are converted into a multi-dimensional path by means of various embedding algorithms and then processed for computation of individual terms of the signature which summarise certain information contained in the data. The signature thus transforms raw data into a set of features which are used in machine learning tasks. We will review current progress in applications of signatures to machine learning problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge