Signature moments to characterize laws of stochastic processes
Paper and Code
Oct 25, 2018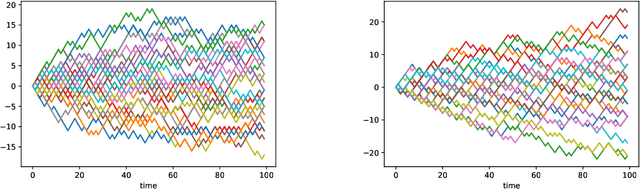
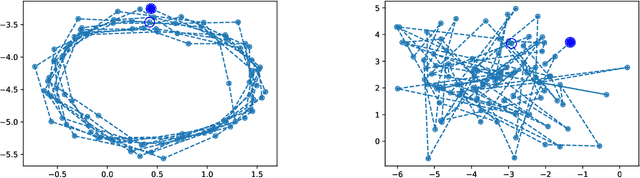
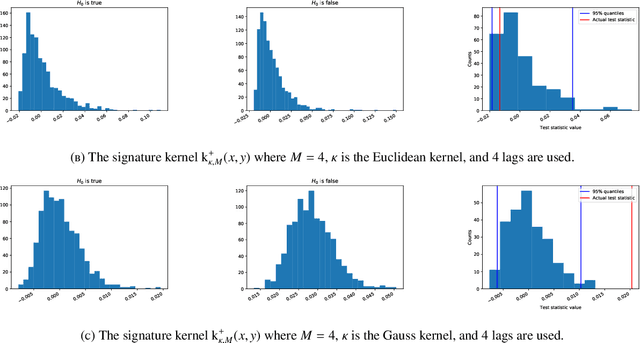
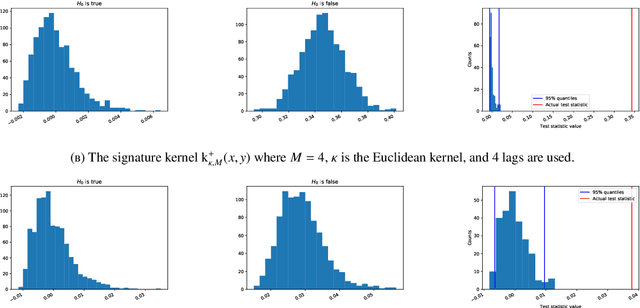
The normalized sequence of moments characterizes the law of any finite-dimensional random variable. We prove an analogous result for path-valued random variables, that is stochastic processes, by using the normalized sequence of signature moments. We use this to define a metric for laws of stochastic processes. This metric can be efficiently estimated from finite samples, even if the stochastic processes themselves evolve in high-dimensional state spaces. As an application, we provide a non-parametric two-sample hypothesis test for laws of stochastic processes.
* 31 pages, 5 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge