Topological fingerprints for audio identification

We present a topological audio fingerprinting approach for robustly identifying duplicate audio tracks. Our method applies persistent homology on local spectral decompositions of audio signals, using filtered cubical complexes computed from mel-spectrograms. By encoding the audio content in terms of local Betti curves, our topological audio fingerprints enable accurate detection of time-aligned audio matchings. Experimental results demonstrate the accuracy of our algorithm in the detection of tracks with the same audio content, even when subjected to various obfuscations. Our approach outperforms existing methods in scenarios involving topological distortions, such as time stretching and pitch shifting.

Intrinsic persistent homology via density-based metric learning

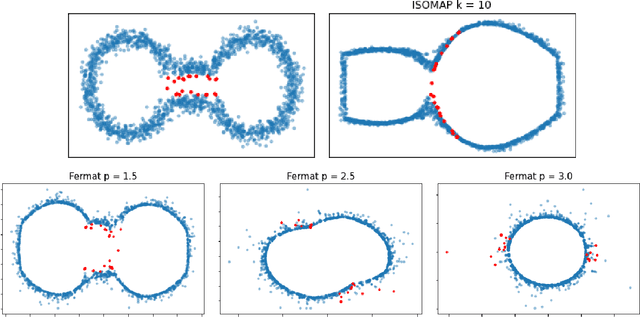
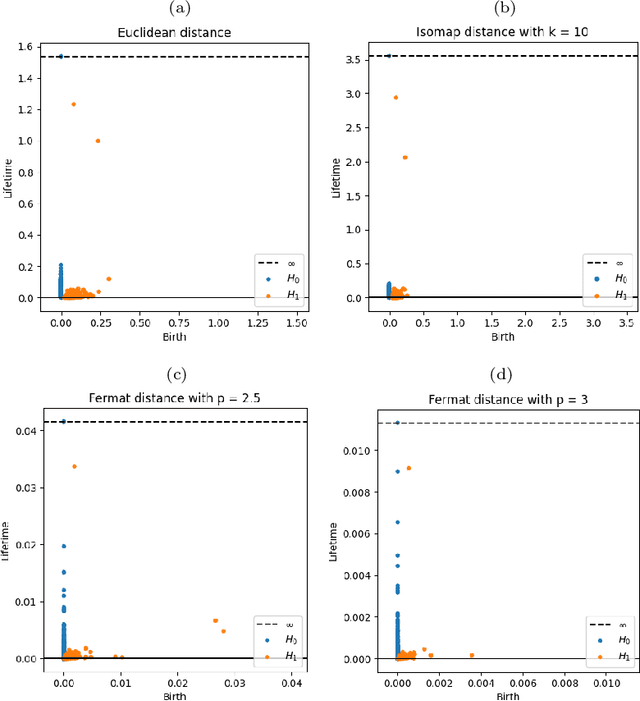
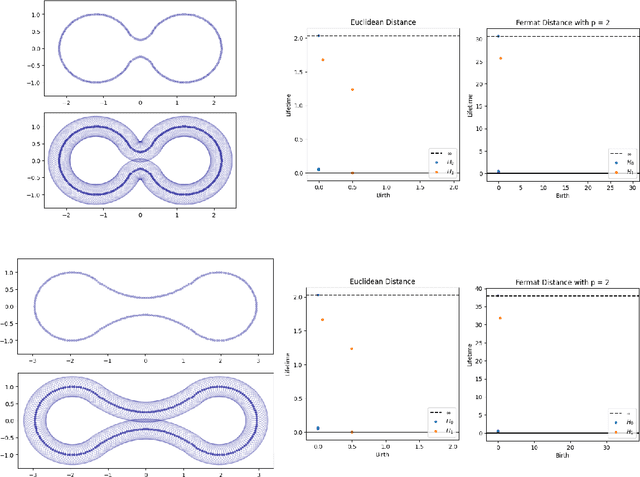
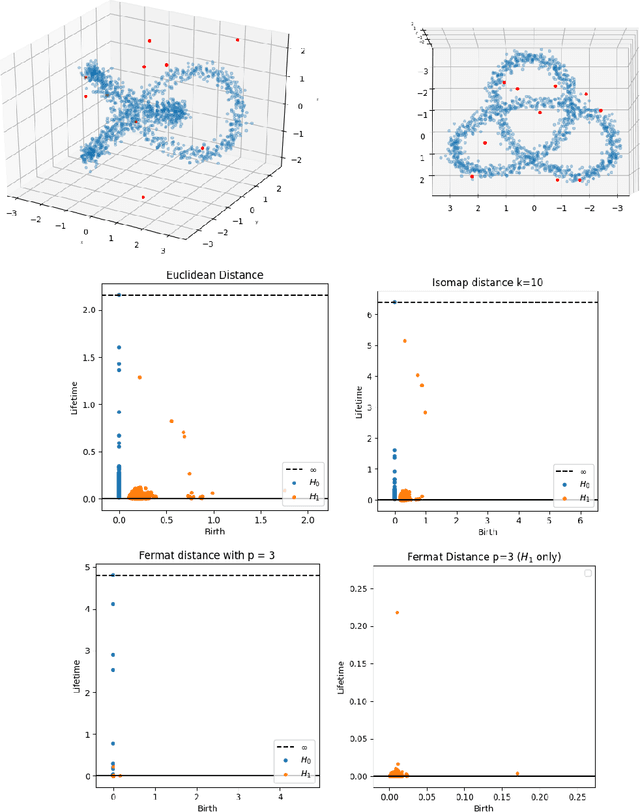
We address the problem of estimating intrinsic distances in a manifold from a finite sample. We prove that the metric space defined by the sample endowed with a computable metric known as sample Fermat distance converges a.s. in the sense of Gromov-Hausdorff. The limiting object is the manifold itself endowed with the population Fermat distance, an intrinsic metric that accounts for both the geometry of the manifold and the density that produces the sample. This result is applied to obtain sample persistence diagrams that converge towards an intrinsic persistence diagram. We show that this method outperforms more standard approaches based on Euclidean norm with theoretical results and computational experiments.