Gabriel Mindlin
Intrinsic persistent homology via density-based metric learning
Dec 11, 2020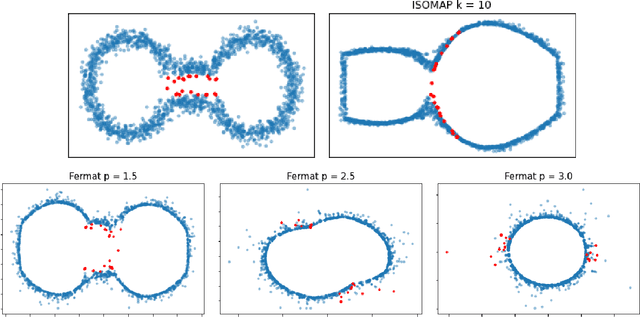
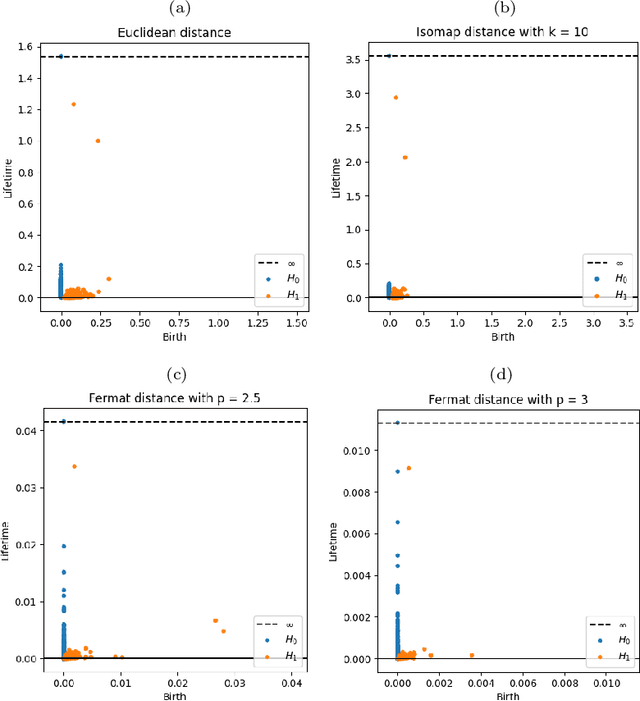
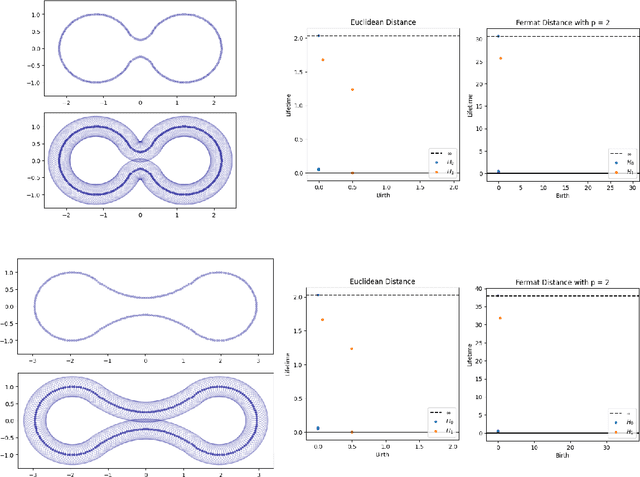
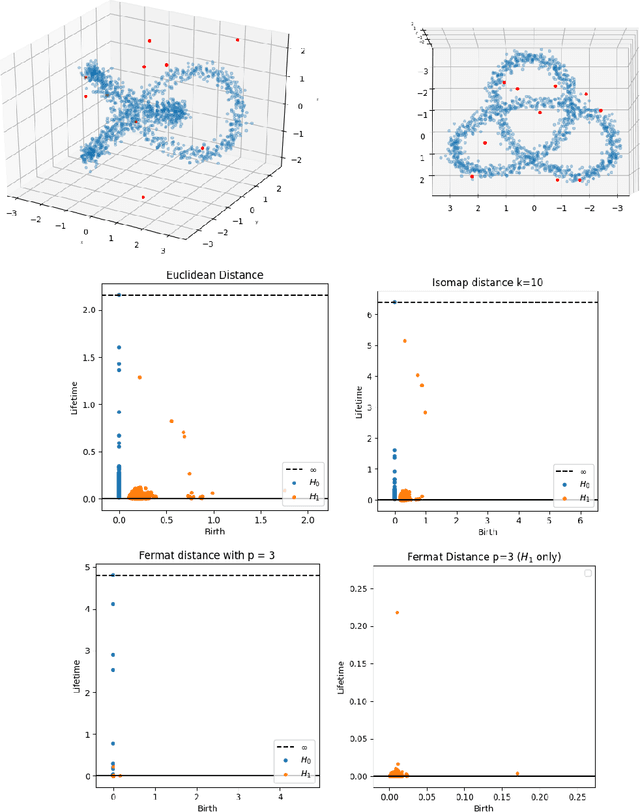
Abstract:We address the problem of estimating intrinsic distances in a manifold from a finite sample. We prove that the metric space defined by the sample endowed with a computable metric known as sample Fermat distance converges a.s. in the sense of Gromov-Hausdorff. The limiting object is the manifold itself endowed with the population Fermat distance, an intrinsic metric that accounts for both the geometry of the manifold and the density that produces the sample. This result is applied to obtain sample persistence diagrams that converge towards an intrinsic persistence diagram. We show that this method outperforms more standard approaches based on Euclidean norm with theoretical results and computational experiments.
Fading of collective attention shapes the evolution of linguistic variants
Nov 29, 2018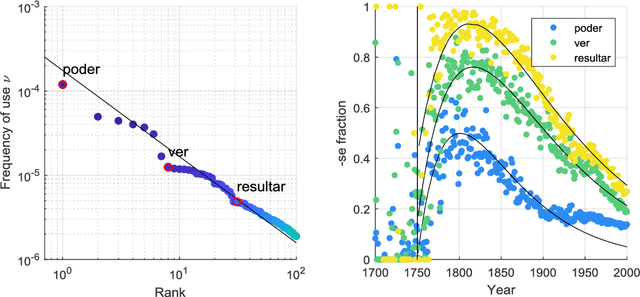
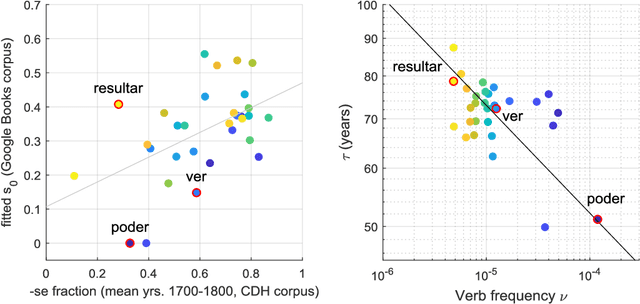
Abstract:Language change involves the competition between alternative linguistic forms (1). Notably, the Spanish past subjunctive comes in two perfectly equivalent variants ended in -ra or -se (2); for instance, in the sentence 'If I were there', the verb can be equally translated to estuviera or estuviese. During a first spontaneous process that began in the Middle Ages, the form -ra migrated from the indicative to the subjunctive, displacing the original -se form (3-5). A second period started with the creation of the Royal Spanish Academy in 1713, which produced a global standardization process that enforced the official spelling of -ra and -se as perfectly interchangeable variants (6). Time series extracted from a massive corpus of books (7) show that this standardization produced a boost in the declining old form -se that eventually faded, leaving -ra as the dominant one in the present time. The time series were successfully fitted by a low dimensional model that integrates two basic collective behaviors: an imitative component, and a fading of collective attention to the institutional regulation. We show that the natural scale over which collective attention fades is inversely proportional to the frequency of use of the verbs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge