Multiscale methods for signal selection in single-cell data

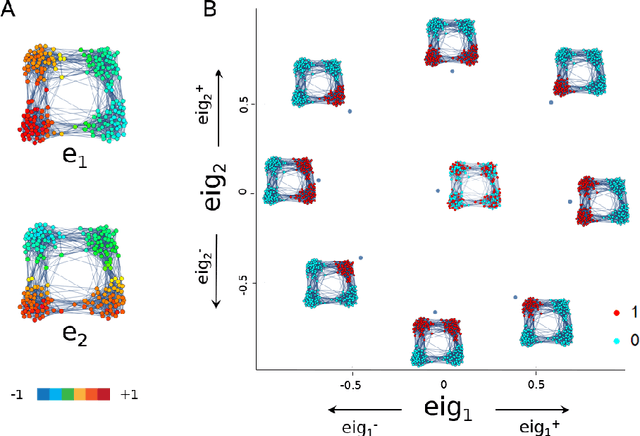
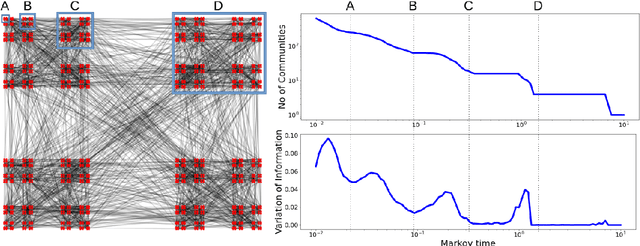
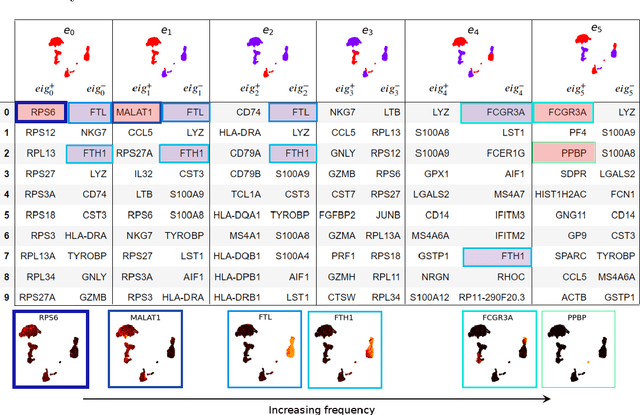
Analysis of single-cell transcriptomics often relies on clustering cells and then performing differential gene expression (DGE) to identify genes that vary between these clusters. These discrete analyses successfully determine cell types and markers; however, continuous variation within and between cell types may not be detected. We propose three topologically-motivated mathematical methods for unsupervised feature selection that consider discrete and continuous transcriptional patterns on an equal footing across multiple scales simultaneously. Eigenscores ($\mathrm{eig}_i$) rank signals or genes based on their correspondence to low-frequency intrinsic patterning in the data using the spectral decomposition of the graph Laplacian. The multiscale Laplacian score (MLS) is an unsupervised method for locating relevant scales in data and selecting the genes that are coherently expressed at these respective scales. The persistent Rayleigh quotient (PRQ) takes data equipped with a filtration, allowing separation of genes with different roles in a bifurcation process (e.g. pseudo-time). We demonstrate the utility of these techniques by applying them to published single-cell transcriptomics data sets. The methods validate previously identified genes and detect additional genes with coherent expression patterns. By studying the interaction between gene signals and the geometry of the underlying space, the three methods give multidimensional rankings of the genes and visualisation of relationships between them.

Statistical and Topological Summaries Aid Disease Detection for Segmented Retinal Vascular Images

Disease complications can alter vascular network morphology and disrupt tissue functioning. Diabetic retinopathy, for example, is a complication of type 1 and 2 diabetus mellitus that can cause blindness. Microvascular diseases are assessed by visual inspection of retinal images, but this can be challenging when diseases exhibit silent symptoms or patients cannot attend in-person meetings. We examine the performance of machine learning algorithms in detecting microvascular disease when trained on either statistical or topological summaries of segmented retinal vascular images. We apply our methods to four publicly-available datasets and find that the fractal dimension performs best for high resolution images. By contrast, we find that topological descriptor vectors quantifying the number of loops in the data achieve the highest accuracy for low resolution images. Further analysis, using the topological approach, reveals that microvascular disease may alter morphology by reducing the number of loops in the retinal vasculature. Our work provides preliminary guidelines on which methods are most appropriate for assessing disease in high and low resolution images. In the longer term, these methods could be incorporated into automated disease assessment tools.