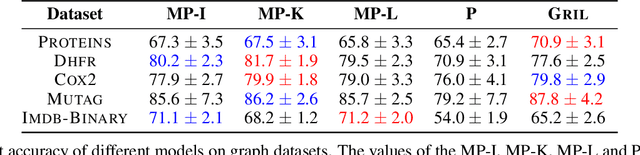
D-GRIL: End-to-End Topological Learning with 2-parameter Persistence

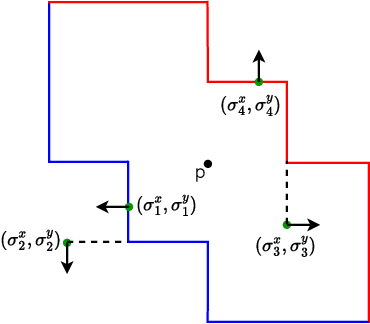
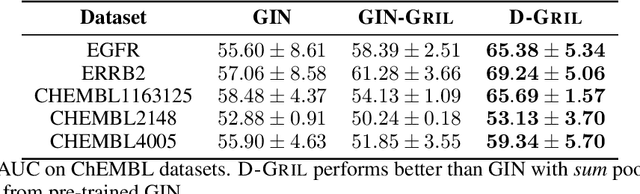
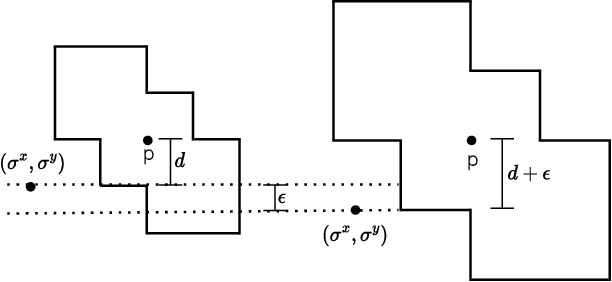
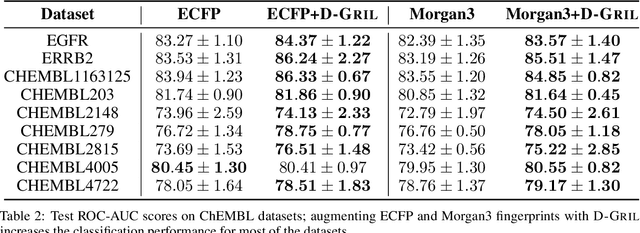
End-to-end topological learning using 1-parameter persistence is well-known. We show that the framework can be enhanced using 2-parameter persistence by adopting a recently introduced 2-parameter persistence based vectorization technique called GRIL. We establish a theoretical foundation of differentiating GRIL producing D-GRIL. We show that D-GRIL can be used to learn a bifiltration function on standard benchmark graph datasets. Further, we exhibit that this framework can be applied in the context of bio-activity prediction in drug discovery.

Optimally Improving Cooperative Learning in a Social Setting

We consider a cooperative learning scenario where a collection of networked agents with individually owned classifiers dynamically update their predictions, for the same classification task, through communication or observations of each other's predictions. Clearly if highly influential vertices use erroneous classifiers, there will be a negative effect on the accuracy of all the agents in the network. We ask the following question: how can we optimally fix the prediction of a few classifiers so as maximize the overall accuracy in the entire network. To this end we consider an aggregate and an egalitarian objective function. We show a polynomial time algorithm for optimizing the aggregate objective function, and show that optimizing the egalitarian objective function is NP-hard. Furthermore, we develop approximation algorithms for the egalitarian improvement. The performance of all of our algorithms are guaranteed by mathematical analysis and backed by experiments on synthetic and real data.

Expressive Higher-Order Link Prediction through Hypergraph Symmetry Breaking

A hypergraph consists of a set of nodes along with a collection of subsets of the nodes called hyperedges. Higher-order link prediction is the task of predicting the existence of a missing hyperedge in a hypergraph. A hyperedge representation learned for higher order link prediction is fully expressive when it does not lose distinguishing power up to an isomorphism. Many existing hypergraph representation learners, are bounded in expressive power by the Generalized Weisfeiler Lehman-1 (GWL-1) algorithm, a generalization of the Weisfeiler Lehman-1 algorithm. However, GWL-1 has limited expressive power. In fact, induced subhypergraphs with identical GWL-1 valued nodes are indistinguishable. Furthermore, message passing on hypergraphs can already be computationally expensive, especially on GPU memory. To address these limitations, we devise a preprocessing algorithm that can identify certain regular subhypergraphs exhibiting symmetry. Our preprocessing algorithm runs once with complexity the size of the input hypergraph. During training, we randomly replace subhypergraphs identified by the algorithm with covering hyperedges to break symmetry. We show that our method improves the expressivity of GWL-1. Our extensive experiments also demonstrate the effectiveness of our approach for higher-order link prediction on both graph and hypergraph datasets with negligible change in computation.

DL3DV-10K: A Large-Scale Scene Dataset for Deep Learning-based 3D Vision

We have witnessed significant progress in deep learning-based 3D vision, ranging from neural radiance field (NeRF) based 3D representation learning to applications in novel view synthesis (NVS). However, existing scene-level datasets for deep learning-based 3D vision, limited to either synthetic environments or a narrow selection of real-world scenes, are quite insufficient. This insufficiency not only hinders a comprehensive benchmark of existing methods but also caps what could be explored in deep learning-based 3D analysis. To address this critical gap, we present DL3DV-10K, a large-scale scene dataset, featuring 51.2 million frames from 10,510 videos captured from 65 types of point-of-interest (POI) locations, covering both bounded and unbounded scenes, with different levels of reflection, transparency, and lighting. We conducted a comprehensive benchmark of recent NVS methods on DL3DV-10K, which revealed valuable insights for future research in NVS. In addition, we have obtained encouraging results in a pilot study to learn generalizable NeRF from DL3DV-10K, which manifests the necessity of a large-scale scene-level dataset to forge a path toward a foundation model for learning 3D representation. Our DL3DV-10K dataset, benchmark results, and models will be publicly accessible at https://dl3dv-10k.github.io/DL3DV-10K/.

GRIL: A $2$-parameter Persistence Based Vectorization for Machine Learning

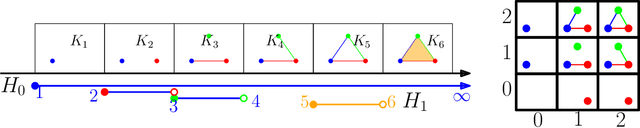
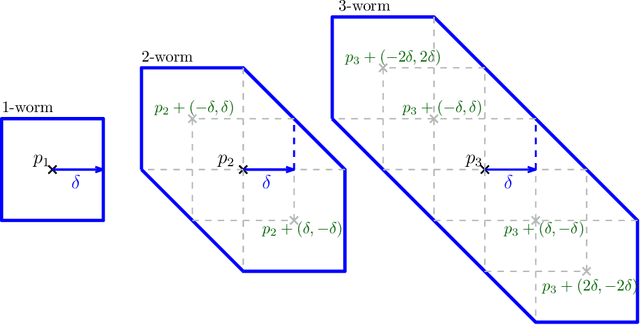
$1$-parameter persistent homology, a cornerstone in Topological Data Analysis (TDA), studies the evolution of topological features such as connected components and cycles hidden in data. It has been applied to enhance the representation power of deep learning models, such as Graph Neural Networks (GNNs). To enrich the representations of topological features, here we propose to study $2$-parameter persistence modules induced by bi-filtration functions. In order to incorporate these representations into machine learning models, we introduce a novel vector representation called Generalized Rank Invariant Landscape \textsc{Gril} for $2$-parameter persistence modules. We show that this vector representation is $1$-Lipschitz stable and differentiable with respect to underlying filtration functions and can be easily integrated into machine learning models to augment encoding topological features. We present an algorithm to compute the vector representation efficiently. We also test our methods on synthetic and benchmark graph datasets, and compare the results with previous vector representations of $1$-parameter and $2$-parameter persistence modules.