Towards Non-Euclidean Foundation Models: Advancing AI Beyond Euclidean Frameworks

In the era of foundation models and Large Language Models (LLMs), Euclidean space is the de facto geometric setting of our machine learning architectures. However, recent literature has demonstrated that this choice comes with fundamental limitations. To that end, non-Euclidean learning is quickly gaining traction, particularly in web-related applications where complex relationships and structures are prevalent. Non-Euclidean spaces, such as hyperbolic, spherical, and mixed-curvature spaces, have been shown to provide more efficient and effective representations for data with intrinsic geometric properties, including web-related data like social network topology, query-document relationships, and user-item interactions. Integrating foundation models with non-Euclidean geometries has great potential to enhance their ability to capture and model the underlying structures, leading to better performance in search, recommendations, and content understanding. This workshop focuses on the intersection of Non-Euclidean Foundation Models and Geometric Learning (NEGEL), exploring its potential benefits, including the potential benefits for advancing web-related technologies, challenges, and future directions. Workshop page: [https://hyperboliclearning.github.io/events/www2025workshop](https://hyperboliclearning.github.io/events/www2025workshop)

Position: Beyond Euclidean -- Foundation Models Should Embrace Non-Euclidean Geometries

In the era of foundation models and Large Language Models (LLMs), Euclidean space has been the de facto geometric setting for machine learning architectures. However, recent literature has demonstrated that this choice comes with fundamental limitations. At a large scale, real-world data often exhibit inherently non-Euclidean structures, such as multi-way relationships, hierarchies, symmetries, and non-isotropic scaling, in a variety of domains, such as languages, vision, and the natural sciences. It is challenging to effectively capture these structures within the constraints of Euclidean spaces. This position paper argues that moving beyond Euclidean geometry is not merely an optional enhancement but a necessity to maintain the scaling law for the next-generation of foundation models. By adopting these geometries, foundation models could more efficiently leverage the aforementioned structures. Task-aware adaptability that dynamically reconfigures embeddings to match the geometry of downstream applications could further enhance efficiency and expressivity. Our position is supported by a series of theoretical and empirical investigations of prevalent foundation models.Finally, we outline a roadmap for integrating non-Euclidean geometries into foundation models, including strategies for building geometric foundation models via fine-tuning, training from scratch, and hybrid approaches.

Shared Global and Local Geometry of Language Model Embeddings

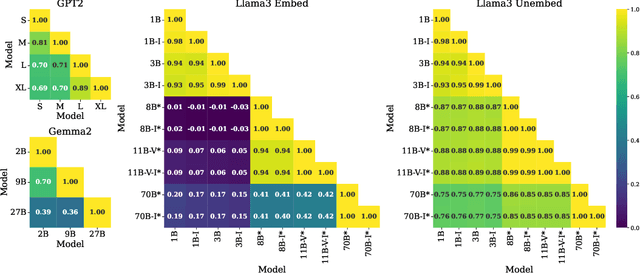
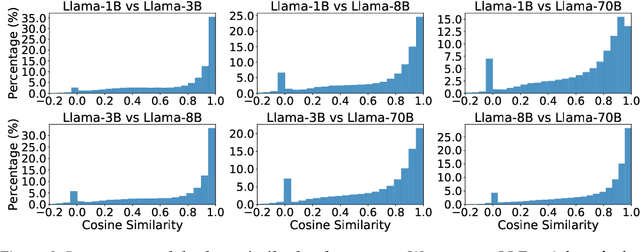
Researchers have recently suggested that models share common representations. In this work, we find that the token embeddings of language models exhibit common geometric structure. First, we find ``global'' similarities: token embeddings often share similar relative orientations. Next, we characterize local geometry in two ways: (1) by using Locally Linear Embeddings, and (2) by defining a simple measure for the intrinsic dimension of each token embedding. Our intrinsic dimension measure demonstrates that token embeddings lie on a lower dimensional manifold. We qualitatively show that tokens with lower intrinsic dimensions often have semantically coherent clusters, while those with higher intrinsic dimensions do not. Both characterizations allow us to find similarities in the local geometry of token embeddings. Perhaps most surprisingly, we find that alignment in token embeddings persists through the hidden states of language models, allowing us to develop an application for interpretability. Namely, we empirically demonstrate that steering vectors from one language model can be transferred to another, despite the two models having different dimensions.

Enhancing the Utility of Higher-Order Information in Relational Learning

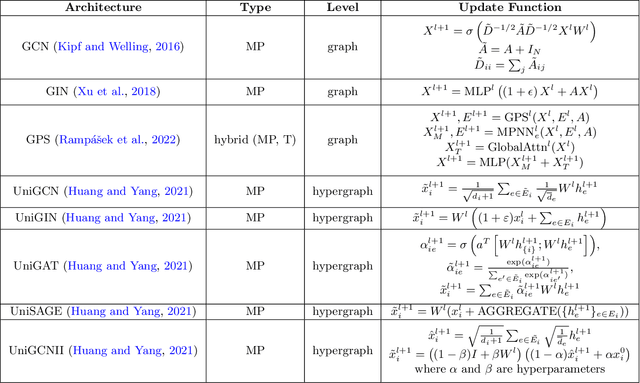
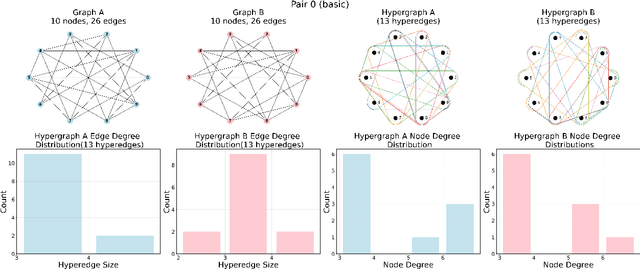
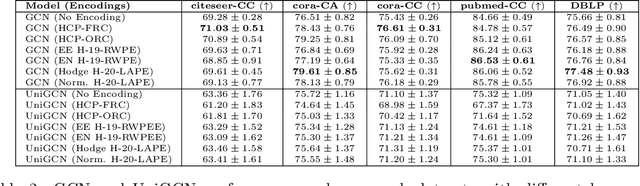
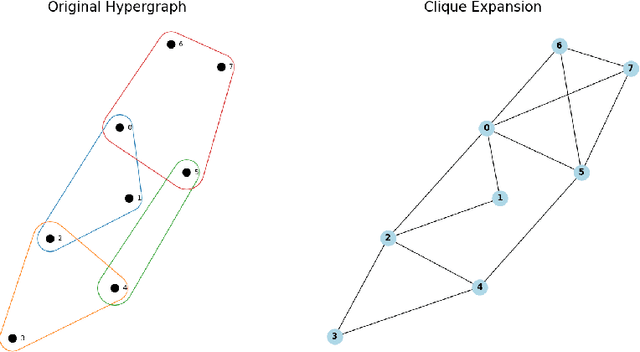
Higher-order information is crucial for relational learning in many domains where relationships extend beyond pairwise interactions. Hypergraphs provide a natural framework for modeling such relationships, which has motivated recent extensions of graph neural net- work architectures to hypergraphs. However, comparisons between hypergraph architectures and standard graph-level models remain limited. In this work, we systematically evaluate a selection of hypergraph-level and graph-level architectures, to determine their effectiveness in leveraging higher-order information in relational learning. Our results show that graph-level architectures applied to hypergraph expansions often outperform hypergraph- level ones, even on inputs that are naturally parametrized as hypergraphs. As an alternative approach for leveraging higher-order information, we propose hypergraph-level encodings based on classical hypergraph characteristics. While these encodings do not significantly improve hypergraph architectures, they yield substantial performance gains when combined with graph-level models. Our theoretical analysis shows that hypergraph-level encodings provably increase the representational power of message-passing graph neural networks beyond that of their graph-level counterparts.

Structured Regularization for Constrained Optimization on the SPD Manifold

Matrix-valued optimization tasks, including those involving symmetric positive definite (SPD) matrices, arise in a wide range of applications in machine learning, data science and statistics. Classically, such problems are solved via constrained Euclidean optimization, where the domain is viewed as a Euclidean space and the structure of the matrices (e.g., positive definiteness) enters as constraints. More recently, geometric approaches that leverage parametrizations of the problem as unconstrained tasks on the corresponding matrix manifold have been proposed. While they exhibit algorithmic benefits in many settings, they cannot directly handle additional constraints, such as inequality or sparsity constraints. A remedy comes in the form of constrained Riemannian optimization methods, notably, Riemannian Frank-Wolfe and Projected Gradient Descent. However, both algorithms require potentially expensive subroutines that can introduce computational bottlenecks in practise. To mitigate these shortcomings, we introduce a class of structured regularizers, based on symmetric gauge functions, which allow for solving constrained optimization on the SPD manifold with faster unconstrained methods. We show that our structured regularizers can be chosen to preserve or induce desirable structure, in particular convexity and "difference of convex" structure. We demonstrate the effectiveness of our approach in numerical experiments.

Unitary convolutions for learning on graphs and groups

Data with geometric structure is ubiquitous in machine learning often arising from fundamental symmetries in a domain, such as permutation-invariance in graphs and translation-invariance in images. Group-convolutional architectures, which encode symmetries as inductive bias, have shown great success in applications, but can suffer from instabilities as their depth increases and often struggle to learn long range dependencies in data. For instance, graph neural networks experience instability due to the convergence of node representations (over-smoothing), which can occur after only a few iterations of message-passing, reducing their effectiveness in downstream tasks. Here, we propose and study unitary group convolutions, which allow for deeper networks that are more stable during training. The main focus of the paper are graph neural networks, where we show that unitary graph convolutions provably avoid over-smoothing. Our experimental results confirm that unitary graph convolutional networks achieve competitive performance on benchmark datasets compared to state-of-the-art graph neural networks. We complement our analysis of the graph domain with the study of general unitary convolutions and analyze their role in enhancing stability in general group convolutional architectures.

Lie Algebra Canonicalization: Equivariant Neural Operators under arbitrary Lie Groups

The quest for robust and generalizable machine learning models has driven recent interest in exploiting symmetries through equivariant neural networks. In the context of PDE solvers, recent works have shown that Lie point symmetries can be a useful inductive bias for Physics-Informed Neural Networks (PINNs) through data and loss augmentation. Despite this, directly enforcing equivariance within the model architecture for these problems remains elusive. This is because many PDEs admit non-compact symmetry groups, oftentimes not studied beyond their infinitesimal generators, making them incompatible with most existing equivariant architectures. In this work, we propose Lie aLgebrA Canonicalization (LieLAC), a novel approach that exploits only the action of infinitesimal generators of the symmetry group, circumventing the need for knowledge of the full group structure. To achieve this, we address existing theoretical issues in the canonicalization literature, establishing connections with frame averaging in the case of continuous non-compact groups. Operating within the framework of canonicalization, LieLAC can easily be integrated with unconstrained pre-trained models, transforming inputs to a canonical form before feeding them into the existing model, effectively aligning the input for model inference according to allowed symmetries. LieLAC utilizes standard Lie group descent schemes, achieving equivariance in pre-trained models. Finally, we showcase LieLAC's efficacy on tasks of invariant image classification and Lie point symmetry equivariant neural PDE solvers using pre-trained models.

Disciplined Geodesically Convex Programming

Convex programming plays a fundamental role in machine learning, data science, and engineering. Testing convexity structure in nonlinear programs relies on verifying the convexity of objectives and constraints. \citet{grant2006disciplined} introduced a framework, Disciplined Convex Programming (DCP), for automating this verification task for a wide range of convex functions that can be decomposed into basic convex functions (atoms) using convexity-preserving compositions and transformations (rules). However, the restriction to Euclidean convexity concepts can limit the applicability of the framework. For instance, many notable instances of statistical estimators and matrix-valued (sub)routines in machine learning applications are Euclidean non-convex, but exhibit geodesic convexity through a more general Riemannian lens. In this work, we extend disciplined programming to this setting by introducing Disciplined Geodesically Convex Programming (DGCP). We determine convexity-preserving compositions and transformations for geodesically convex functions on general Cartan-Hadamard manifolds, as well as for the special case of symmetric positive definite matrices, a common setting in matrix-valued optimization. For the latter, we also define a basic set of atoms. Our paper is accompanied by a Julia package SymbolicAnalysis.jl, which provides functionality for testing and certifying DGCP-compliant expressions. Our library interfaces with manifold optimization software, which allows for directly solving verified geodesically convex programs.

Graph Pooling via Ricci Flow

Graph Machine Learning often involves the clustering of nodes based on similarity structure encoded in the graph's topology and the nodes' attributes. On homophilous graphs, the integration of pooling layers has been shown to enhance the performance of Graph Neural Networks by accounting for inherent multi-scale structure. Here, similar nodes are grouped together to coarsen the graph and reduce the input size in subsequent layers in deeper architectures. In both settings, the underlying clustering approach can be implemented via graph pooling operators, which often rely on classical tools from Graph Theory. In this work, we introduce a graph pooling operator (ORC-Pool), which utilizes a characterization of the graph's geometry via Ollivier's discrete Ricci curvature and an associated geometric flow. Previous Ricci flow based clustering approaches have shown great promise across several domains, but are by construction unable to account for similarity structure encoded in the node attributes. However, in many ML applications, such information is vital for downstream tasks. ORC-Pool extends such clustering approaches to attributed graphs, allowing for the integration of geometric coarsening into Graph Neural Networks as a pooling layer.

Hardness of Learning Neural Networks under the Manifold Hypothesis

The manifold hypothesis presumes that high-dimensional data lies on or near a low-dimensional manifold. While the utility of encoding geometric structure has been demonstrated empirically, rigorous analysis of its impact on the learnability of neural networks is largely missing. Several recent results have established hardness results for learning feedforward and equivariant neural networks under i.i.d. Gaussian or uniform Boolean data distributions. In this paper, we investigate the hardness of learning under the manifold hypothesis. We ask which minimal assumptions on the curvature and regularity of the manifold, if any, render the learning problem efficiently learnable. We prove that learning is hard under input manifolds of bounded curvature by extending proofs of hardness in the SQ and cryptographic settings for Boolean data inputs to the geometric setting. On the other hand, we show that additional assumptions on the volume of the data manifold alleviate these fundamental limitations and guarantee learnability via a simple interpolation argument. Notable instances of this regime are manifolds which can be reliably reconstructed via manifold learning. Looking forward, we comment on and empirically explore intermediate regimes of manifolds, which have heterogeneous features commonly found in real world data.